Привязка линейно-угловых ходов

Под привязкой разомкнутого линейно-углового хода понимают включение в ход двух пунктов с известными координатами (это начальный и конечный исходные пункты хода) и измерение на этих пунктах углов между направлением с известным дирекционным углом (αнач и αкон) и первой (последней) стороной хода; эти углы называются примычными. Как уже отмечалось ранее, если на начальном или (и) конечном пункте хода примычный угол не измеряется, то имеет место частичная (полная) координатная привязка хода.

Привязка замкнутого линейно-углового хода - это включение в ход одного пункта с известными координатами и измерение на этом пункте примычного угла, то-есть, угла между направлением с известным дирекционным углом и первой стороной хода.

Кроме этих стандартных ситуаций встречаются случаи, когда линейно-угловой ход начинается или заканчивается на пункте с неизвестными координатами. В таких случаях возникает дополнительно задача определения координат этого пункта.

Самый простой способ определения координат одного пункта - геодезические засечки; если вблизи определяемого пункта есть несколько известных пунктов, то, выполнив k угловых и (или) линейных измерений (k>2), можно вычислить искомые координаты по стандартным алгоритмам. Если такой возможности нет, то возникают особые случаи привязки; рассмотрим некоторые из них.

Снесение координат с вершины знака на землю. На рис.2.20: P - определяемый пункт, T1, T2, T3 - пункты с известными координатами, которые можно использовать лишь в качестве визирных целей. С пункта P можно измерить только два угла по программе обратной угловой засечки, что недостаточно; кроме того, при малом расстоянии между пунктами P и T1, угол засечки очень маленький и точность засечки невысокая. Закладывают два временных пункта A1 и A2 и измеряют расстояния b1 и b2 и углы β1, β2, β3, β4, β5, β6.

Таким образом, общее число измерений равно 8, а количество неизвестных - 6 (координаты трех пунктов). Обработку этого геодезического построения необходимо выполнять уравниванием по МНК;

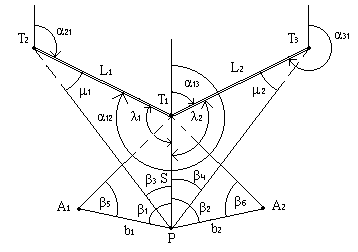
Рис.2.20

приближенное решение можно получить по конечным формулам, приведенным ниже:

вычисление расстояния s (s = T1P) два раза: из треугольников PA1T1 и PA2T2 и затем среднего из двух:

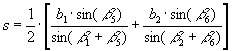
решение обратной геодезической задачи между пунктами T1 и T2 (вычисление α12, L1) и T1 и T3 (вычисление α13, L2),

вычисление углов μ1 и μ2 из треугольников PT2T1 и PT3T1:

;

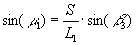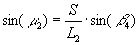
вычисление углов λ1 и λ2 из треугольников PT2T1 и PT3T1:

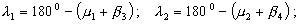
вычисление дирекционного угла линии T1P:

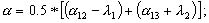
решение прямой геодезической задачи из пункта T на пункт P:

Привязка линейно-углового хода к стенным маркам. Стенные марки закладываются в цокольный этаж или в стену капитального здания; конструкции их бывают различными и одна из них показана на рис.7.1-г (раздел 7.2). Закладка стенных марок и определение их координат выполняется при создании геодезических сетей на территории населенных пунктов и промышленных предприятий; в дальнейшем эти марки играют роль опорных пунктов в последующих геодезических построениях.

Привязка линейно-углового хода может быть выполнена к двум, трем или более стенным маркам.

Схема привязки хода к двум маркам A и B показана на рис.2.21.

На линии AB с помощью рулетки измеряется отрезок S, и координаты точки P находятся из решения прямой геодезической задачи по формулам:

где α - дирекционный угол направления AB.

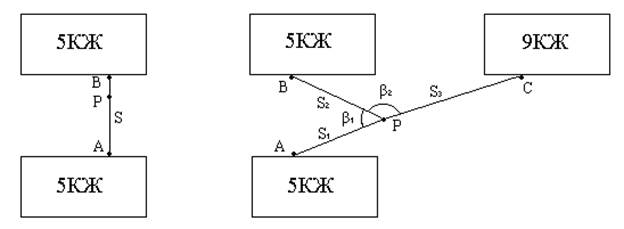
Рис.2.21 Рис.2.22

Схема привязки к трем маркам A, B, C показана на рис.2.22. С помощью рулетки измеряются расстояния S1, S2, S3 и решается многократная линейная засечка; для большей надежности можно измерить углы β1 и β2 и решить комбинированную засечку.

В качестве примычного направления с известным дирекционным углом можно использовать либо направление на одну из стенных марок, либо направление на какой-нибудь другой пункт с известными координатами.

Кроме метода засечек при привязке ходов к стенным маркам применяют также полярный метод и метод редуцирования. В [28] на стр. 195 - 201 приведено подробное описание этих методов, а так же даны числовые примеры.