Прямая угловая засечка
Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы β1 и β2 измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.2.6).

Рис.2.6
Исходные данные: XA, YA, αAC,
XB, YB, αBD
Измеряемые элементы: β 1 , β2
Неизвестные элементы: X , Y
Если αAC и αBD не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D .
Графическое решение. От направления AC отложить с помощью транспортира угол β1 и провести прямую линию AP; от направления BD отложить угол β2 и провести прямую линию BP ; точка пересечения этих прямых является искомой точкой P.
Аналитическое решение. Приведем алгоритм варианта, соответствующий общему случаю засечки:
вычислить дирекционные углы линий AP и BP
 (2.14) ,
(2.14) ,
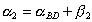 (2.15)
(2.15)
написать два уравнения прямых линий
для линии AP Y - YA= tgα1 * ( X - XA ),
для линии BP Y - YB= tgα2 * ( X - XB ) (2.16)
решить систему двух уравнений и вычислить неизвестные координаты X и Y:
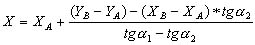 (2.17) ,
(2.17) ,
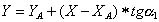 (2.18)
(2.18)
Частным случаем прямой угловой засечки считают тот случай, когда углы β1 и β2 измерены от направлений AB и BA, причем угол β1 - правый, а угол β2 - левый (в общем случае засечки оба угла - левые) - рис.2.7.
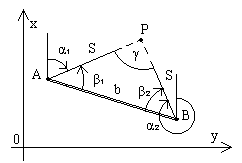
Рис.2.7
Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения при этом будет такой:
решить обратную задачу между пунктами A и B и получить дирекционный угол αAB и длину b линии AB,
вычислить угол γ при вершине P, называемый углом засечки,
 (2.19)
(2.19)
используя теорему синусов для треугольника APB:
 (2.20)
(2.20)
вычислить длины сторон AP (S1) и BP (S2) ,
вычислить дирекционные углы α1 и α2:
 (2.21)
(2.21)
решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P.
Для вычисления координат X и Y в частном случае прямой угловой засечки можно использовать формулы Юнга:
 (2.22)
(2.22)
От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол αAB линии AB и затем вычислить углы в треугольнике APB при вершинах A и B
 BAP = αAB - ( αAC + β1 ) и
BAP = αAB - ( αAC + β1 ) и  ABP = ( αBD + β2 ) - αBA .
ABP = ( αBD + β2 ) - αBA .
Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия:
вычисление дирекционных углов α1 и α2 ,
введение местной системы координат X'O'Y' с началом в пункте A и с осью O'X', направленной вдоль линии AP, и пересчет координат пунктов A и B и дирекционных углов α1 и α2 из системы XOY в систему X'O'Y' (рис.2.8):
X'A = 0 , Y'A = 0 ,
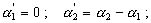 (2.23) ,
(2.23) ,
 (2.24) ,
(2.24) ,
запись уравнений линий AP и BP в системе X'O'Y' :
 (2.26)
(2.26)
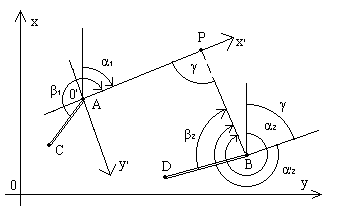
Рис.2.8
и совместное решение этих уравнений:
 (2.27)
(2.27)
перевод координат X' и Y' из системы X'O'Y' в систему XOY:
 (2.28)
(2.28)
Так как Ctgα2' = - Ctgγ и угол засечки γ всегда больше 0о, то решение (2.27) всегда существует.
Линейная засечка
От пункта A с известными координатами XA, YA измерено расстояние S1 до определяемой точки P, а от пункта B с известными координатами XB, YB измерено расстояние S2 до точки P .
Графическое решение. Проведем вокруг пункта A окружность радиусом S1 (в масштабе чертежа), а вокруг пункта B - окружность радиусом S2; точка пересечения окружностей является искомой точкой; задача имеет два решения, так как две окружности пересекаются в двух точках (рис.2.9).
Исходные данные: XA, YA, XB, YB,
Измеряемые элементы: S1, S2,
Неизвестные элементы: X, Y.
Аналитическое решение. Рассмотрим два алгоритма аналитического решения, один - для ручного счета (по способу треугольника) и один - для машинного счета.
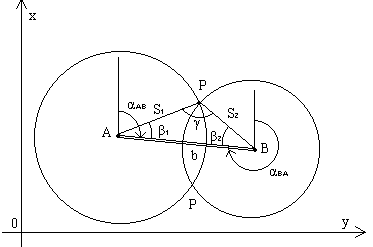
Рис.2.9
Алгоритм ручного счета состоит из следующих действий:
решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов:
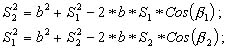 (2.29)
(2.29)
вычисление угла засечки γ
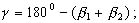 (2.30)
(2.30)
вычисление дирекционных углов сторон AP и BP:
пункт P справа от линии AB
 (2.31)
(2.31)
пункт P слева от линии АВ
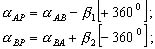 (2.32)
(2.32)
решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P:
1-е решение
 (2.33)
(2.33)
2-е решение
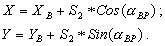 (2.34)
(2.34)
Результаты обоих решений должны совпадать.
Алгоритм машинного решения линейной засечки состоит из следующих действий:
решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
введение местной системы координат X'O'Y' с началом в точке A и осью O'X', направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X'O'Y':
 (2.35)
(2.35)
запись уравнений окружностей в системе X'O'Y':
 (2.36)
(2.36)
и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого:
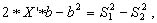 (2.37)
(2.37)
откуда
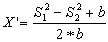 (2.38)
(2.38)
и
 (2.39)
(2.39)
Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак "-", если справа, то "+".
пересчет координат X' и Y' точки P из системы X'O'Y' в систему XOY по формулам (2.2):
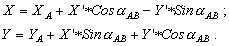
Дата добавления: 2016-02-02; просмотров: 1015;
