Определение координат засечками

Засечкой называется метод определения координат отдельной точки измерением элементов, связывающих ее положение с исходными пунктами.

Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения. Засечки различают прямые, обратные и комбинированные. В прямой засечке измерения выполняют на исходных пунктах (рис. 6.6 a, г); в обратной – на определяемом пункте (рис. 6.6 б, д); в комбинированной – на исходных и определяемом пунктах (рис. 6.6 в). В зависимости от вида измерений засечки бывают угловые (рис. 6.6 a, б, в), линейные (рис. 6.6 г), линейно-угловые (рис. 6.6 д). Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами.

Рассмотрим вычисление координат в некоторых засечках.

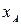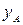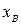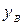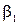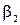Прямая угловая засечка. На исходных пунктах A и B с координатами , , , . (рис. 6.6 а)измеряют углы и . При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:

; .

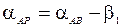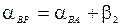Дирекционные углы с координатами связаны формулами обратной геодезической задачи

; .

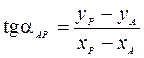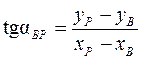Решая эти уравнения относительно x_p и y_p, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):

; (6.5)

.

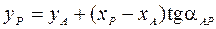Для контроля ординату y_P вычисляют вторично по формуле:

.

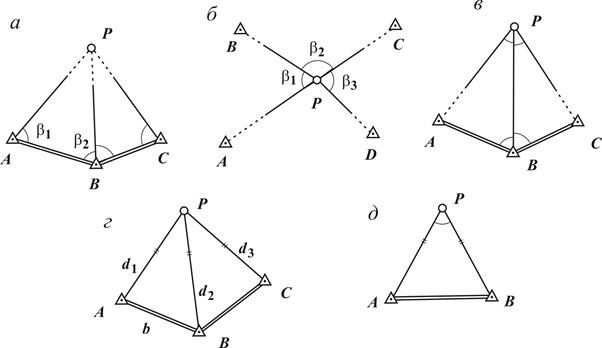
Рис. 6.6. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая

Если один из дирекционных углов или 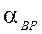близок к 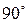или 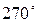, то вместо формул (6.5 – 6.7) вычисления выполняют по формулам

;

.

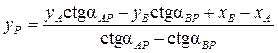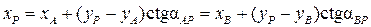Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние.

Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):

; .

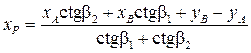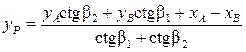Обратная угловая засечка. На определяемой точке P (рис. 6.6 б) измеряют углы 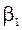и между направлениями на исходные пункты A, B и C. При этом исходные пункты выбирают такие, чтобы они с точкой P не оказались на одной окружности или вблизи нее. Координаты точки P вычисляют по формулам Гаусса (6.5 - 6.7), предварительно вычислив дирекционные углы:

; .

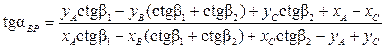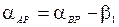Для контроля измеряют избыточный угол 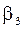и вычисляют координаты, используя другую пару измеренных углов.

Линейная засечка. Для определения координат точки Р (рис. 6.6 г) измеряют расстояния d₁, d₂. По формуле косинусов (6.1) находят углы треугольника АРВ. Вычисляют дирекционный угол a_АР = a_АВ - ÐA, а затем по формулам прямой геодезической задачи - искомые координаты

x_P = x_A + d₁cosa_АР; y_P = y_A + d₁sina_АР.

Для контроля измеряют избыточное расстояние d₃ и вычисляют координаты из другого треугольника ВРС.

Измерение углов

Определения

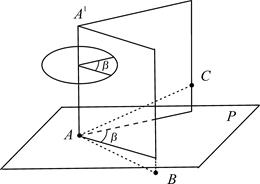
Горизонтальным углом называют проекцию b пространственного угла ÐCAB (рис. 7.1) на горизонтальную плоскость P. Для измерения горизонтального угла, образуемого направлениями AС и AВ, необходимо круг с делениями расположить горизонтально, совместив его центр с отвесной линией AA¢, проходящей через вершину угла A, и определить число делений круга между проекциями направлений AС и AВ на плоскость круга.

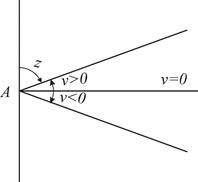
Вертикальные углы - это углы, расположенные в вертикальной плоскости (рис. 7.2). Углом наклона линии называют угол n между направлением линии и её проекцией на горизонтальную плоскость. Углы наклона выше горизонта - положительные, ниже горизонта - отрицательные. Зенитное расстояние – угол z между направлением в зенит и направлением линии.

Рис. 7.1. Горизонтальный угол¢	Рис. 7.2. Вертикальные углы

Горизонтальные и вертикальные углы измеряют теодолитами.