Вывод закона преломления света по аналогии с теннисным мячиком

Декарт попытался вывести закон преломления света, основываясь на предположении о том, что луч света преломляется при переходе из одной среды в другую подобно тому, как меняет направление движения теннисный мячик, пробивающий экран из тонкой ткани. Допустим, что такой мячик ударяется о ткань наклонно со скоростью v_A . При этом он потеряет часть скорости и после прохождения сквозь ткань будет иметь скорость v_B < v_A , но мы не ожидаем, что это столкновение приведет к изменению компоненты скорости мячика, направленной вдоль экрана. Можно нарисовать прямоугольный треугольник, катеты которого будут соответствовать перпендикулярной и параллельной компонентам начальной скорости мячика по отношению к экрану, а гипотенуза будет обозначать полную скорость v_A . Если исходная траектория расположена под углом i к перпендикуляру к поверхности, тогда компонента скорости параллельно ткани будет равна v_A sin i (см. рис. 20). Аналогично, если после пробивания преграды путь мячика идет дальше под углом r к тому же перпендикуляру, то параллельная поверхности компонента скорости составит v_B sin r . Вслед за Декартом предполагая, что пробивающий ткань мячик меняет лишь поперечную, а не продольную скорость, получаем:

и, следовательно,

где n является отношением

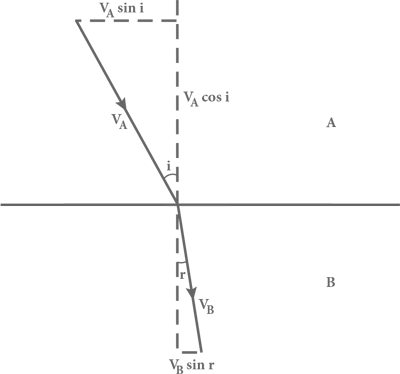
Рис. 20. Скорости теннисного мячика. Горизонтальная линия обозначает экран из ткани, которую пробивает теннисный мячик с начальной скоростью v_A и скоростью после события v_B . Прямые линии со стрелками показывают масштаб и направления этих скоростей. На этом чертеже путь мячика претерпевает излом, становясь ближе к перпендикуляру к поверхности, как это происходит в случае, когда луч света попадает в более плотную среду. Это показывает, что пробивание мячиком тканевого экрана явно уменьшает компоненту его скорости, направленную вдоль поверхности, в противоположность тому, что предполагал Декарт.

Уравнение (1) известно как закон Снеллиуса, верно описывающий случай преломления света. К несчастью, аналогия между светом и теннисным мячиком теряет смысл при рассмотрении уравнения (2), дающего нам величину n : дело в том, что для теннисных мячей v_B меньше, чем v_A , и уравнение (2) дает n < 1, тогда как в случае, когда свет проникает из воздушной среды внутрь стекла или воды, получается n > 1. Плохо и другое: нет оснований полагать, что для теннисного мячика отношение v_B /v_A действительно не зависит от углов i и r , поэтому пользы от уравнения (1) в таком виде мало.

Как доказал Ферма, когда свет проходит границу между средой, где его скорость равна v_A , и другой средой, где скорость равна v_B , показатель преломления n в действительности равен отношению v_A /v_B , а не v_B /v_A . Декарт не знал, что скорость света конечна, и предложил необоснованное объяснение тому, почему n больше единицы в том случае, когда среда A – воздух, а среда B – вода. Для задач XVII в., таких как декартова теория радуги, это было неважно, так как n считался не зависящим от угла падения, что хоть и не верно для мячиков, верно для света, и к тому же значение показателя бралось из наблюдений, а не выводилось на основе измерений скорости света в различных средах.