Закон сохранения импульса

Пусть два движущихся объекта с массами m ₁ и m ₂ сталкиваются лоб в лоб. Если за некоторый короткий промежуток времени δt объект 1 воздействует на объект 2 с силой F , то за этот промежуток времени второй объект подвергнется действию ускорения a ₂, которое согласно Второму закону механики Ньютона будет удовлетворять равенству m ₂a ₂ = F . Его скорость v 2 после этого изменится на величину:

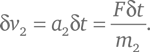
Согласно Третьему закону Ньютона второе тело подействует на первое с силой – F , которая равна по величине, но противоположна по направлению (на что указывает знак «минус»), поэтому в тот же промежуток времени скорость первого объекта v ₁ изменится в направлении, противоположном δv ₂, на величину:

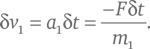
Тогда суммарное изменение общего импульса m 1v 1 + m 2v 2 равно:

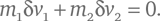
Конечно, два объекта могут оставаться в соприкосновении в течение более продолжительного времени, на протяжении которого сила не остается постоянной, но, так как суммарный импульс сохраняется в каждый малый промежуток времени, он сохраняется и все то время, пока длится столкновение.

Массы планет

В эпоху Ньютона было известно, что четыре тела Солнечной системы обладают спутниками: у Юпитера, Сатурна и Земли есть свои спутники, а все планеты в то же время сами являются спутниками Солнца. По Закону всемирного тяготения тело массой M оказывает воздействие силой F = GMm /r ² на спутник массой m на расстоянии r (где G – мировая гравитационная постоянная), поэтому по Второму закону Ньютона центростремительное ускорение, которое испытывает этот спутник, вычисляется как a = F /m = GM /r ². Значение константы G и общие размеры Солнечной системы еще не были известны во времена Ньютона, но эти неизвестные величины не фигурируют в выражениях для отношений масс, рассчитываемых исходя из отношений расстояний и отношений центростремительных ускорений. Если два спутника тел с массами M ₁ и M ₂ обнаруживаются на некоторых расстояниях r ₁ и r ₂ от своих центральных тел, для которых известно их отношение r ₁/r ₂, а также отношение их центростремительных ускорений a ₁/a ₂, то отношение масс двух тел можно найти по формуле:

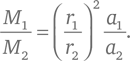
В частности, если спутник движется с постоянной скоростью v по круговой орбите радиусом r , его орбитальный период равен T = 2πr /v , поэтому его центростремительное ускорение v ²/r равняется a = 4π ²r /T ², отношение ускорений двух спутников a ₁/a ₂ = (r ₁/r ₂)/(T ₂/T ₁) 2, а отношение масс, выведенное из орбитальных периодов и отношений расстояний, равно:

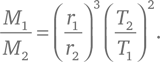
К 1687 г. все соотношения расстояний между планетами и Солнцем были хорошо известны, а зная по результатам наблюдений максимальные угловые расстояния между Юпитером и его спутником Каллисто, а также Сатурном и его спутником Титаном (который Ньютон называл «гюйгенсовым спутником»), можно было вывести отношения расстояния от Каллисто до Юпитера к расстоянию от Юпитера до Солнца, а также расстояния от Титана до Сатурна к расстоянию от Сатурна до Солнца. Расстояние от Луны до Земли было точно измерено в единицах земного диаметра, но не в отношении к расстоянию между Землей и Солнцем – тогда это значение еще не было известно. Ньютон использовал грубую прикидку для расстояний между Землей и Луной, а также между Землей и Солнцем, и использованные им значения несли значительную ошибку. Не считая этой конкретной проблемы, отношения скоростей и центростремительных ускорений планет и спутников хорошо выводились его методом из их известных орбитальных периодов обращения (на самом деле Ньютон взял для расчета период обращения Венеры, а не Юпитера или Сатурна, но это не повлияло на результат, поскольку соотношения расстояний от Солнца Венеры, Юпитера и Сатурна были достоверно известны). Как мы говорили в главе 14, полученные Ньютоном отношения масс Юпитера и Сатурна к массе Солнца были достаточно точны, тогда как рассчитанное им отношение массы Земли к массе Солнца было совершенно ошибочным.

Аристотель. Метафизика / Пер. А. В. Кубицкого. – М.; Л.: Соцэкгиз, 1934. С. 23.

Диоген Лаэртский. О жизни, учениях и изречениях знаменитых философов / Пер. с др. – гр. М. Л. Гаспарова. – М.: Мысль, 1986.

Фрагменты ранних греческих философов. Ч. I. От эпических теокосмогоний до возникновения атомистики / Под ред. А. В. Лебедева. – М.: Наука, 1989. С. 117. (Далее – Фрагменты.)

Богомолов А. С. Античная философия (История философии). – 2‑е изд. – М.: Высшая школа, 2006. С. 67.

Антология мировой философии: Античность. – М. 2001. С. 48.

Как указывает в своей работе «Вселенная Платона» Грегори Властос (Gregory Vlastos, Plato’s Universe, University of Washington Press, Seattle, 1975), наречие, образованное от слова «kosmos», использовал Гомер в значении «социально подобающий» или «морально совершенный». Этот смысл лег в основу понятия «косметика» в современном английском и других языках. Тот факт, что его использовал Гераклит, отражает точку зрения древних греков, которая заключалась в том, что мир в целом таков, каким он и должен быть. Также от него происходят родственные понятия «космос» и «космология».

Фрагменты. С. 217.

Там же. С. 379.

Там же. С. 344.

Богомолов А. С. Указ. соч. С. 163.

Там же. С. 176.

Аристотель. Метафизика. С.54.

Полное собрание творений Платона: в 15 т. Т. 1 / Под ред. С. А. Жебелева, Л. П. Карсавина, Э. Л. Радлова. – Петербург: Academia, 1923. С. 182–183.

См., напр.: Аристотель. Метафизика. С. 62.

Платон. Диалоги. – М.: Мысль, 1986.

Томас Д. Собрание стихотворений 1934–1953 / Пер. с англ. В. Бетаки. – Б. м. Salamandra P. V. V., 2010. С. 16.

Фрагменты. С. 173.

Я писал об этом в главе «Замечательные теории» в книге «Мечты об окончательной теории» (Dreams of a Final Theory, Pantheon, New York, 1992), переизданной с новым послесловием издательством Vintage, New York, 1994.

Alberto A. Martínez, The Cult of Pythagoras – Man and Myth (University of Pittsburgh Press, Pittsburgh, Pa., 2012).

Аристотель. Метафизика. С. 26–27.

Там же.

Аристотель. Сочинения: в 4 т. Т. 2. – М.: Мысль, 1978. С. 167.

[1]Лат. «сведе́ние к невозможности» – прием опровержения в философии. – Прим. ред.

Платон. Диалоги. 147 d – e.

На самом деле, как это обсуждается в техническом замечании 2, что бы ни доказал Теэтет и что бы ни приписывали ему «Начала», существует только пять возможных выпуклых правильных многогранников. На примере правильного полиэдра в «Началах» доказывается, что существует только пять комбинаций длин сторон каждой грани полиэдра и количества граней, которые имеют общие точки. Но там не доказано, что для каждой комбинации этих чисел существует только единственный выпуклый правильный многогранник.

Аристотель. Сочинения: в 4 т. Т. 3. – М.: Мысль, 1981. С. 140.

Платон. Избранное. – М.: АСТ, 2006.

Вигнер Е. Непостижимая эффективность математики в естественных науках // Этюды о симметрии / Пер. с англ. – М.: Мир, 1971.

[2]По др.‑гр. στοά ποικίλη – «расписной портик». – Прим. ред.

J. Barnes, The Complete Works of Aristotle – The Revised Oxford Translation (Princeton University Press, Princeton, N.J., 1984).

R. J. Hankinson, The Cambridge Companion to Aristotle, ed. J. Barnes (Cambridge University Press, Cambridge, 1995), p. 165.

Аристотель. Сочинения. Т. 3. С. 86.

Там же. С. 82.

Там же. С. 508.

Там же. С. 279–280.

Там же. С. 138.

Там же.

Греческое слово κίνησις, которое обычно переводится как «движение», в действительности имеет более общее значение, относящееся к любому изменению. Таким образом, классификация причин движения у Аристотеля включает в себя не только изменения положения тела, но и любое изменение. Греческое слово φορά употребляется, только когда идет речь о перемене местоположения, и обычно переводится как «перемещение».

Аристотель. Сочинения. Т. 3. С. 206.

Там же. С. 349.

Чосер Дж. Кентерберийские рассказы/Пер. И. Кашкина, О. Румера. – М.: Вече, 2011. С. 8.

Thomas Kuhn, Remarks on Receiving the Laurea // L'Anno Galileiano (Edizioni LINT, Trieste, 1995).

David C. Lindberg, The Beginnings of Western Science (University of Chicago Press, Chicago, Ill., 1992), pp. 53–54.

Op. cit. seem 2‑nd ed. (University of Chicago Press, Chicago, Ill., 2007), p. 65.

Michael R. Matthews, Introduction to: «The Scientific Background to Modern Philosophy» (Hackett, Indianapolis, Ind., 1989).

Это наименование я позаимствовал из ведущей современной работы по этому периоду: Alexander to Actium (University of California Press, Berkeley, 1990).

Я считаю, что это замечание первоначально принадлежало Джорджу Сартону.

В английском переводе Симпликий о работах Стратона см.: M. R. Cohen and I. E. Drabkin, A Source Book в Greek Science (Harvard University Press, Cambridge, Mass., 1948), pp. 211–212.

H. Floris Cohen, How Modern Science Came into the World (Amsterdam University Press, Amsterdam, 2010), p. 17.

О новейших исследованиях взаимосвязи технологии с физикой см.: Bruce J. Hunt, Pursuing Power and Light: Technology and Physics from James Watt to Albert Einstein (Johns Hopkins University Press, Baltimore, Md., 2010).

Описание экспериментов Филона см.: G. I. Ibry‑Massie and P. T. Keyser, Greek Science of the Hellenistic Era (Routledge, London, 2002), pp. 216–219.

В древности обычно считалось, что люди видят предметы потому, что лучи света исходят из глаза и касаются видимого объекта, как если бы зрение ощупывало предмет. Далее я неявно предполагаю, что читатель разделяет современную точку зрения о том, что мы видим потому, что свет идет от видимого предмета к глазу наблюдателя. К счастью, при анализе отражения и преломления света нет разницы, в какую именно сторону движется луч.

Это цитата из греческого манускрипта 6 в. до н. э. в английском переводе: Ibry‑Massie и Keyser, Greek Science of the Hellenistic Era.

См. Таб. V. 1, с. 233, в переводе «Оптики» Птолемея: A. Mark Smith, «Ptolemy's Theory of Visual Perception» // Transactions of the American Philosophical Society 86, Part 2 (1996).

Архимед. Сочинения. – M, 1962. С. 328.

«Пробирных дел мастер» – полемика Галилея с его противниками‑иезуитами, выраженная в форме письма к тайному камергеру Его Святейшества Вирджинио Чезарини. Как мы увидим в главе 11, в этом сочинении Галилео критиковал верную точку зрения Тихо Браге и иезуитов на то, что кометы находятся дальше от Земли, чем Луна (цитата в этом месте приводится по изданию: Галилео Галилей. Пробирных дел мастер / Пер. Ю. А. Данилова. – М.: Наука, 1987).

[3]Переводы на русский язык выходили под именем Диоген Лаэрций, однако в настоящее время принято использовать имя Диоген Лаэртский. – Прим. науч. ред.

Платон. Собрание сочинений: в 4 т. Т. 3. – М.: Мысль, 1994. С. 433–434.

Erwin Schrödinger, Shearman Lectures at University College London, May 1948, опубликовано Nature and the Greeks (Cambridge University Press, Cambridge, 1954).

Alexandre Koyré, From the Closed World to the Infinite Universe (Johns Hopkins University Press, Baltimore, Md., 1957), p. 159.

Фрагменты. С. 171.

S. Greenblatt, The Answer Man: An Ancient Poem Was Rediscovered and the World Swerved // The New Yorker , 8 aug. 2011, pp. 28–33.

Пьер Гассенди – французский священник и философ, который пытался связать атомистические теории Эпикура и Лукреция с христианством.

Гиббон Э. Закат и падение Римской империи: в 7 т. Т. 2/Пер. с англ. – М.: ТЕРРА – Книжный клуб, 2008. С. 525.

Гиббон Э. Указ. соч. С. 104.

Коперник Н. О вращениях небесных сфер/Пер. проф. И. Н. Веселовского. – М.: Наука, 1964. С. 15.

Лактанций. Божественные установления. Книги I–VII. – СПб.: Издательство Олега Абышко, 2007. Кн. III, разд. 24. С. 223–224.

Новый Завет. Послание к колоссянам, 2:8.

Блаженный Августин. Исповедь. – СПб.: Наука, 2013. С.56.

Augustine, Retractions, Book I. Chapter 1, trans. M. I. Bogan (Catholic University of America Press, Washington, D. C., 1968), p. 10.

Гиббон Э. Указ. соч. С. 382.

Эта глава частично основывается на моей статье «Миссия астрономии» (The Missions of Astronomy), New York Review of Books 56, 16 (22 Oct. 2009): 19–22; напечатанной в: The Best American Science and Nature Writing, ed. Freeman Dyson (Houghton Mifflin Harcourt, Boston, Mass., 2010), pp. 23–31; The Best American Science Writing, ed. Jerome Groopman (HarperCollins, New York, 2010), pp. 272–281.

Гомер. Илиада / Пер. Н. Гнедича. Песнь XXII, 27–31.

Гомер. Одиссея / Пер. В. Жуковского. Песнь V, 271–277.

Диоген Лаэртский. О жизни, учениях и изречениях знаменитых философов. – М.: АСТ, Астрель, 2011. С. 61.

Такую интерпретацию одной из строк работы Гераклита см.: D. R. Dicks в Early Greek Astronomy to Aristotle (Cornell University Press, Ithaca, N.Y., 1970).

Более правильно сказать, что так определяется синодический лунный месяц. А 27‑дневный промежуток времени, за который Луна возвращается в ту же самую точку по отношению к неподвижным звездам, называется сидерическим лунным месяцем.

Этого не происходит каждый месяц, поскольку плоскость орбиты, по которой Луна обращается вокруг Земли, слегка наклонена по отношению к плоскости орбиты обращения Земли вокруг Солнца. Луна пересекает плоскость земной орбиты дважды в месяц, но затмение происходит в полнолуние, когда Земля расположена между Солнцем и Луной, лишь раз в каждые 18 лет. (Имеется в виду повторение лунного затмения, когда Луна расположена в том же самом созвездии, так называемый цикл сароса , в то время как всего за 18 лет происходит в среднем 28 лунных затмений. – Прим. пер. )

Равноденствие – это момент, когда Солнце в своем видимом движении на фоне звезд пересекает небесный экватор. Говоря современным языком, это тот момент, когда вектор от Земли к Солнцу становится перпендикулярен земной оси. В точках с различной долготой на земной поверхности это происходит в разное локальное время суток, поэтому для наблюдателей из разных географических точек момент равноденствия может выпасть на разные даты. Все сказанное относится и к наблюдению фаз Луны.

Платон. Избранное. – М.: АСТ, 2006.

Филон Иудей (Александрийский). О неразрушимости и вечности мира // Браш М. Классики философии. – СПб., 1907.

Важное значение работ Параменида и Анаксагора в формировании астрономии как науки см.: Daniel W. Graham, Science Before Socrates – Parmenides, Anaxagoras, and the New Astronomy (Oxford University Press, Oxford, 2013).

Freeman, The Ancilla to the Pre‑Socratic Philosophers (Harvard University Press, Cambridge, Mass., 1966), p. 23.

О. Нейгебауэр отмечает в своей работе «История древней математической астрономии» (in O. Neugebauer, A History of Ancient Mathematical Astronomy , Springer‑Verlag, New York, 1975, pp. 1093–94), что вывод Аристотеля о форме Земли на основании формы наблюдаемой тени на Луне необоснован, так как существует бесконечное множество возможных форм Земли и Луны, которые могли бы дать в результате такую же форму тени.

Аристотель. Сочинения: в 4 т. Т. 3. – М.: Мысль, 1981. С. 340.

Самуэль Элиот Морисон приводит тот же самый аргумент в своем жизнеописании Христофора Колумба «Адмирал моря‑океана» (Admiral of the Ocean Sea , Little Brown, Boston, Mass., 1942), чтобы опровергнуть общепринятый предрассудок, будто бы до экспедиции Колумба не знали, что Земля имеет форму шара. Дебаты при кастильском дворе насчет того, финансировать или нет планирующуюся экспедицию Колумба, имели предметом не форму Земли, а ее размер . Колумб считал, что Земля достаточно маленькая, чтобы он мог дойти из Испании до восточных берегов Азии, не исчерпав запасы воды и еды. Он ошибся в оценке размера Земли, но, конечно, неожиданное появление Американского континента между Европой и Азией спасло ему жизнь.

Фрагменты. С. 173.

Аристотель. Сочинения. Т.3. С. 325.

Архимед. Сочинения. С. 328.

Веселовский И.Н. Аристарх Самосский – Коперник античного мира // Историко‑астрономические исследования. 1961. Вып. 7.

В «Псаммите» Архимед сделал интереснейшее замечание: Аристарх определил, что «Солнце занимает 1/720 часть зодиака». Таким образом, угловой размер видимого с Земли диска Солнца равняется произведению 1/720 на 360°, то есть 0,5°, что близко к истинному значению 0,519°. Архимед также заявил, что он удостоверил это число собственными наблюдениями. Но, как мы видели, в той работе Аристарха, которая дошла до нашего времени, используется значение углового размера Луны 2°, и одновременно он отмечает, что видимые размеры лунного и солнечного дисков одинаковые. Действительно ли Архимед привел цитату из более поздней, не сохранившейся работы Аристарха или же использовал результат собственных измерений, приписав заслугу их получения Аристарху? Я слышал мнение изучавших историю вопроса, что дело могло быть в ошибке переписчика или переводчика текста, но это предположение выглядит необоснованным. Как мы уже отметили, Аристарх из своих изменений углового диаметра Луны заключил, что расстояние от нее до Земли лежит между 30 и 45/2 лунных диаметров, а такой вывод нельзя сделать, если принять угловой диаметр Луны равным 0,5°. Современная тригонометрия утверждает, с другой стороны, что если принять угловой диаметр лунного диска за 2°, то расстояние между Луной и Землей составит 28,6 единиц лунного диаметра, каковое число действительно лежит в диапазоне между 45/2 и 30. («Псаммит» не являлся серьезным трудом, посвященным астрономии, в нем Архимед демонстрировал свой способ производить вычисления с очень большими числами, такими как, например, количество песчинок, достаточное, чтобы наполнить всю сферу неподвижных звезд.)

Архимед. Сочинения. С.359.

[4]Автор имеет в виду карусель, на которой помимо общего вращения происходит вращение посадочных мест. – Прим. ред.

Там же. С. 337.

Аристотель. Сочинения. Т. 3. С. 336.

Существует знаменитое устройство эпохи античности, известное как Антикитерский механизм. Найдено оно было в 1901 г. ныряльщиками – ловцами губок у берегов острова Антикитера, расположенного в Средиземном море между Критом и континентальной Грецией. Предполагается, что он утонул в море во время кораблекрушения в период 150–100 гг. до н. э. Хотя Антикитерский механизм превратился в изуродованный коррозией кусок бронзы, ученым удалось понять, как он работал, проанализировав его конструкцию при помощи рентгеновских лучей. По всей видимости, это был не планетарий, а разновидность механического календаря, который мог указать наблюдаемое расположение Луны и планет в зодиакальных созвездиях на любую дату. Самое важное, о чем говорит Антикитерский механизм, – это тот факт, что его сложный передаточный механизм из множества шестерней служит свидетельством высокого уровня развития техники в эпоху эллинизма.

Цицерон. Диалоги: О государстве. О законах. / Пер. В.О. Горенштейна, прим. И. Н. Веселовского и В. О. Горенштейна, ст. С. Л. Утченко; отв. ред. С. Л. Утченко. (Серия «Литературные памятники»). – М.: Наука, 1966.

Этот эксперимент был реконструирован в наше время. См.: Albert van Helden, Measuring the Universe – Cosmic Dimensions from Aristarchus to Halley (University of Chicago Press, Chicago, Ill., 1983), pp. 10–13.

Птолемей К. Альмагест: Математическое сочинение в тринадцати книгах. – М.: Наука, 1998. С. 269.

Небесная широта – это угловое расстояние от звезды до линии эклиптики. Что касается долготы, то на Земле мы отмеряем ее от Гринвичского меридиана, а небесная долгота есть угловое расстояние, измеренное по малому кругу на фиксированной небесной широте, от звезды до небесного меридиана, на котором находится Солнце в день весеннего равноденствия.

Другую точку зрения см.: O. Neugebauer, A History of Ancient Mathematical Astronomy (Springer‑Verlag, New York, 1975), pp. 288, 577.

Альмагест. С.214.

Основываясь на собственных наблюдениях звезды Регул, Птолемей в своем «Альмагесте» привел значение смещения в один градус примерно за 100 лет.

Cleomedes, Lectures on Astronomy, ed. and trans. A. C. Bowen и R. B. Todd (University of California Press, Berkeley and Los Angeles, 2004).

Эратосфену просто повезло. Сиена была расположена не точно к югу от Александрии (ее долгота 32,9° в. д., а Александрии – 29.9° в. д.), и в полдень во время летнего солнцестояния солнце не расположено в Сиене точно в зените, но на угловом расстоянии 0,4° от вертикали. Оба этих отклонения взаимно скомпенсировали друг друга. На самом деле Эратосфен измерил отношение длины окружности Земли к расстоянию от Александрии до тропика Рака (который Клеомед называл летним тропическим кругом) (или северный тропик. – Прим. пер. ), параллели, на которой во время летнего солнцестояния солнце действительно расположено точно в зените в полдень. Александрия расположена на широте 31,2°, а широта тропика Рака 23.5°, что меньше широты Александрии на 7,7°, поэтому длина окружности Земли в действительности равна 360°/7,7°, что в 46,75 раз больше расстояния между Александрией и тропиком Рака, и лишь чуть‑чуть меньше, чем число 50, названное Эратосфеном.

Для ясности, когда в этой главе я говорю о планетах, я имею в виду только пять из них: Меркурий, Венеру, Марс, Юпитер и Сатурн.

Мы можем видеть связь дней недели с названием планет и именами богов в названиях дней недели в английском языке. Суббота, воскресенье и понедельник (Saturday, Sunday, Monday) явно связаны с Сатурном, Солнцем и Луной. Названия вторника, среды, четверга и пятницы (Tuesday, Wednesday, Thursday, Friday) связаны с именами немецких богов, у которых, вероятно, были латинские эквиваленты: Тир ассоциировался с Марсом, Вотан – с Меркурием, Тор – с Юпитером, а Фригга – с Венерой.

G. W. Burch, The Counter‑Earth // Osiris 11, 267 (1954).

Аристотель. Метафизика. С. 27.

Симпликий. Комментарий к четырем книгам трактата Аристотеля «О небе». Комментарий ко второй книге // Историко‑философский ежегодник. 2004. М., 2005. С. 12.

Модель Евдокса очень хорошо описана в: James Evans, The History and Practice of Ancient Astronomy (Oxford University Press, Oxford, 1998), pp. 307–309.

Метафизика. Книга XII. Гл.8.

См.: On Aristotle, On the Heavens 3.1–7 (Cornell University Press, Ithaca, N.Y., 2005), 493.1‑497.8, pp. 33–36; trans. I. Mueller.

Эта симметрия была открыта в ходе эксперимента в 1956 г. физиками Ву Цзяньсюн и Янгом Чжэньнином.

Метафизика. Книга XII. Гл. 8.

См.: D. R. Dicks, Early Greek Astronomy to Aristotle (Cornell University Press, Ithaca, N.Y., 1970), р. 202. Дикс высказывает различные версии, почему Аристотель допустил эти ошибки.

Mueller, Simplicius, On Aristotle's «On the Heavens 2.10–2.14», 519.9–519.11, р. 59.

За год, состоящий из 365,25 дней, Земля на самом деле совершает 366,25 оборота вокруг своей оси. Кажется, что Солнце поворачивается вокруг Земли только 365,25 раза, потому что в то же самое время, когда Земля поворачивается 366,4 раза вокруг своей оси, она совершает один оборот вокруг Солнца в том же самом направлении, что и дает 365,4 видимых оборота Солнца вокруг Земли. Поскольку Земле требуется 365,25 дней, состоящих из 24 часов, чтобы совершить 366,25 оборотов относительно звезд, для одного оборота Земли вокруг своей оси необходимо (365,25 x 24 часа)/366,25 или 23 часа 56 минут и 4 секунды. Это число называется звездными сутками.

Mueller, 504.19‑504.30, р 43.

См.: Book I of Otto Neugebauer, A History of Ancient Mathematical Astronomy (Springer‑Verlag, New York, 1975).

Начиная с Птолемея и до наших дней видимая яркость звезд в каталогах описывается термином «звездная величина». Значение звездной величины возрастает, когда яркость уменьшается. Одна из самых ярких звезд – Сириус – имеет звездную величину –1,4, яркая Вега имеет звездную величину 0, а звезды, еле заметные невооруженным глазом, относятся к шестой звездной величине. В 1856 г. астроном Норман Погсон сравнил измеренную видимую светимость определенного количества звезд со звездными величинами, которые исторически приписывались им, и на основании этого сделал вывод, что, если звездная величина одной звезды больше, чем у другой, на пять единиц, то эта звезда в 100 раз тусклее.

[5]Теории Коперника. – Прим. пер.

В одном из немногих намеков на происхождение эпицикла Птолемей в начале Книги XII «Альмагеста» благодарит Аполлония из Перга за доказательство теоремы, связанной с использованием эпицикла и эксцентра в расчетах видимого движения Солнца.

Использование эксцентра в теории движения Солнца может рассматриваться как подвид эпицикла, в котором прямая линия из центра эпицикла до Солнца всегда параллельна прямой линии между Землей и центром солнечного деферента, таким образом, центр солнечной орбиты смещен от Земли. То же самое применимо и к Луне, и к другим планетам.

Птолемей не использовал термин «эквант». Вместо него он прибегал к термину «бисекция эксцентра», ссылаясь на тот факт, что центр деферента должен помещаться в середине линии, связывающей эквант и Землю.

В личной переписке Дж. Смита.

То же самое положение остается верным и когда добавляются эксцентры и экванты. Наблюдения влияют только на соотношение между расстоянием до Земли и экванта из центра деферента и радиусами деферента и эпицикла отдельно для каждой планеты.

См. «Альмагест» Птолемея G. J. Toomer (Duckworth, London, 1984), Book V, Chapter 13, рр. 247–251. Также см.: O. Neugebauer, A History of Ancient Mathematical Astronomy, P. 1 (Springer Verlag, Berlin, 1975), рр. 100–103.

Barrie Fleet, Simplicius on Aristotle «Physics 2» (Duckworth, London, 1997), 291.23–292.29, рр. 47–48.

Цит. по: Duhem, To Save the Phenomena, pp. 20–21.

Там же.

См.: S. Weinberg, Can Science Explain Everything? Anything? in New York Review of Books 48, 9 (31 мая, 2001): 47–50. Reprint: Australian Review (2001); in Portuguese, Folha da S. Paolo (2001); in French, La Recherche (2001); The Best American Science Writing, ed. M. Ridley and A. Lightman (HarperCollins, New York, 2002); The Norton Reader (W. W. Norton, New York, December 2003); Explanations – Styles of Explanation in Science, ed. John Cornwell (Oxford University Press, London, 2004), 23–38; in Hungarian, Akadeemia 176, No. 8: 1734–1749 (2005); S. Weinberg, Lake Views – This World and the Universe (Harvard University Press, Cambridge, Mass., 2009).

Связь астрологии с вавилонской традицией хорошо иллюстрируется словами из Оды XI первой книги «Од» Горация: «Ты гадать перестань: нам наперед знать не дозволено, // Левконоя, какой ждет нас конец. Брось исчисления // Вавилонских таблиц! Лучше терпеть, что бы ни ждало нас…» (пер. по кн.: Гораций. Оды. Эподы. Сатиры. Послания. – М.: Художественная литература, 1970. С. 57). На латыни это место звучит еще лучше: «Tu ne quaesieris – scire nefas – quem mihi, quem tibi, finem di dederint, Leuconoë, nec Babylonios temptaris numeros, ut melius, quidquid erit, pati…»

Русский пер. цит. по: Нейфах Г. Гармония Божественного творения. Взаимоотношения науки и религии. www.polemics.ru

Это письмо цитирует Евтихий, позже ставший патриархом Александрии. См.: E. M. Forster, Pharos and Pharillon (Knopf, New York, 1962), рр. 21–22. Менее содержательный перевод на англ.: Gibbon, Decline and Fall, Chapter 51.

P. K. Hitti, History of the Arabs (Macmillan, London, 1937), р. 315.

D. Gutas, Greek Thought, Arabic Culture – The Graeco‑Arabic Translation Movement in Baghdad and Early Abbasid Society (Routledge, London, 1998), рр. 53–60.

Его полное имя Абу́ Абдулла́х Муха́ммад ибн Муса́ аль‑Хорезми́. Полные арабские имена слишком длинны, поэтому я в основном использую сокращенные варианты, под которыми известен тот или иной человек. Также я опускаю надстрочные знаки, например, ā, которые не имеют никакого значения для читателя, который (как я сам) не знаком с арабским.

[6]Algorithm – латинизированная форма имени ученого. – Прим. ред.

Альфраганус – это латинизированное имя, под которым аль‑Фаргани был известен в средневековой Европе. Далее в тексте все латинизированные имена арабов будут даваться, как и в данном случае, в скобках.

Абу Рейхан Бируни Геодезия (Определение границ мест для уточнения расстояний между населенными пунктами)/Исследования, перевод и примечания П. Г. Булгакова. Избранные произведения Т. 3. – Ташкент: «ФАН», 1966. С. 217.

Аль‑Бируни использовал и десятеричную, и шестидесятитеричную систему счиления. Он привел высоту горы как 652;3;18 локтя, то есть 652 + 3/60 + 18/3600, что соответствует 652,055 локтя в десятеричной системе счисления.

Цит. по: P. Duhem, To Save the Phenomena, р. 29.

Цит. по: R. Arnaldez and A. Z. Iskandar in The Dictionary of Scientific Biography (Scribner, New York, 1975), Vol. 12, р. 3, 7.

G. J. Toomer, Centaurus 14, 306 (1969).

[7]Моше бен Маймон. Путеводитель растерянных. – Маханаим, Мосты культуры/Гешарим, 2010.

Здесь Маймон приводит цитату из Псалтири, псалом 113:24.

[8]От арабского слова «алкали», означающего поташ. – Прим. пер.

[9]Устройство для дистилляции спирта или, проще говоря, самогонный аппарат. – Прим. пер.

По этому поводу см.: Масуд Э. Наука и ислам (E. Masood, Science and Islam, (Icon Books, London, 2009).

[10]То есть кругов, секущих сферу таким образом, что геометрический центр круга совпадает с геометрическим центром сферы. – Прим. пер.

N. M. Swerdlow, Proceedings of the American Philosophical Society 117, 423 (1973).

О том, что Коперник узнал об этой геометрической конструкции из арабских источников, см.: F. J. Ragep, History of Science 14, 65 (2007).

См.: Toby E. Huff, Intellectual Curiosity and the Scientific Revolution (Cambridge University Press, Cambridge, 2011), Chapter 5.

По кн.: Фицджеральд Э. Рубайят Омара Хайяма/Пер. с англ. О. Румера. – СПб.:Издательский дом Санкт‑Петербургского государственного университета, 2009.

Цит. по: Jim al‑Khalili, The House of Wisdom (Penguin, New York, 2011), p. 188.

Al‑Ghazali's Tahafut al‑Falasifah, trans. Sabih Ahmad Kamali (Pakistan Philosophical Congress, Lahore, 1958).

Al‑Ghazali, Fatihat al‑Ulum, trans. I. Goldheizer, Studies on Islam, ed. Merlin L. Swartz (Oxford University Press, 1981), quotation, p. 195.

См.: Lynn White Jr., Medieval Technology and Social Change (Oxford University Press, Oxford, 1962), Chapter 2.

Peter Dear, Revolutionizing the Sciences‑European Knowledge and Its Ambitions, 1500–1700, 2nd ed. (Princeton University Press, Princeton, N.J., and Oxford, 2009), p. 15.

Запрещенные положения cм.: Edward Grant – A Source Book in Medieval Science, ed. E. Grant (Harvard University Press, Cambridge, Mass., 1974), pp. 48–50.

Ibid. P. 47.

Процитировано в: David C. Lindberg, The Beginnings of Western Science (University of Chicago Press, Chicago, Ill., 1992), p. 241.

Ibid.

Nicole Oresme, Le livre du ciel et du monde, на французском и перевод на английский A. D. Menut и A. J. Denomy (University of Wisconsin Press, Madison, 1968), p. 369.

Из статьи «Buridan» в Dictionary of Scientific Biography, ed. Charles Coulston Gillespie (Scribner, New York, 1973), Vol. 2, pp. 604–605.

См.: статью Пиаже в: The Voices of Time, ed. J. T. Fraser (Braziller, New York, 1966).

Oresme, Le livre.

Библия, Ветхий завет, Книга Бытия, 1:6.

Oresme, Le livre, pp. 537–539.

A.C. Crombie, Robert Grosseteste and the Origins of Experimental Science – 1100–1700 (Clarendon, Oxford, 1953).

См.: T. C. R. McLeish // Nature 507, 161–163 (13 March, 2014).

Роджер Б. Избранное / Под ред. И. В. Лупандина. – М.: Издательство францисканцев, 2005.

[11]За исключением дат рождения и смерти Томаса Брадварина, в скобках указаны годы, на которые приходится творческий расцвет упомянутых ученых. – Прим. пер.

Гайденко В. П., Смирнов Г. А. Западноевропейская наука в Cредние века: Общие принципы и учение о движении. – М.: Наука, 1989. С. 322.

См.: ссылку 28 к IV части.

Доминго де Сото цитирует в английском переводе W. A. Wallace, Isis 59, 384 (1968).

Более поздний исследователь Джордж Хартманн (1489–1564) утверждал, что видел письмо Региомонтана, содержащее следующее высказывание: «Движение звезд должно несколько отличаться от движения Земли». Если это правда, то Региомонтан, возможно, предвосхитил работы Коперника, хотя его высказывание также соответствовало пифагорейской модели, в которой Земля и Солнце обращаются вокруг центра мира.

Цит. по: Duhem, To Save the Phenomena, pp. 49–50.

Баттерфилду принадлежит словосочетание «виговская интерпретация истории», которое он использовал, когда критиковал историков, которые оценивают прошлое по его вкладу в существующее в настоящем времени. Но когда речь идет о научной революции, Баттерфилд был не менее «вигом», чем я сам.

Herbert Butterfield, The Origins of Modern Science, rev. ed. (Free Press, New York, 1957), p. 7.

Reappraisals of the Scientific Revolution, ed. D. C. Lindberg and R. S. Westfall (Cambridge University Press, Cambridge, 1990), and Rethinking the Scientific Revolution, ed. M. J. Osler (Cambridge University Press, Cambridge, 2000).

Steven Shapin, The Scientific Revolution (University of Chicago Press, Chicago, Ill., 1996), p. 1.

Pierre Duhem. The System of the World: A History of Cosmological Doctrines from Plato to Copernicua (Hermann, Paris, 1913).

См.: Edward Rosen, Three Copernican Treatises (Farrar, Straus and Giroux, New York, 1939), или Noel M. Swerdlow, The Derivation and First Draft of Copernicus's Planetary Theory: A Translation of the Commentariolus with Commentary // Proceedings of the American Philosophical Society 117, 423 (1973).

См., напр.: N. Jardine, Journal of the History of Astronomy 13, 168 (1982).

O. Neugebauer, Astronomy and History – Selected Essays (Springer‑Verlag, New York, 1983), Vol. 40.

Как уже было упомянуто в главе 8, существует один особый случай простейшей версии теории Птолемея (с одним эпициклом для каждой планеты и без эпицикла для Солнца), который эквивалентен простейшей версии теории Коперника, отличаясь только точкой зрения на Солнечную систему. В этом особом случае каждый из деферентов внутренних планет совпадает с орбитой Солнца вокруг Земли, в то время как все радиусы эпициклов внешних планет равны расстоянию от Земли до Солнца. Радиусы эпициклов внутренних планет и радиусы деферентов внешних планет в этом особом случае теории Птолемея совпадают с радиусами орбит планет в теории Коперника.

О важности этой закономерности для Коперника см.: Bernard R. Goldstein, Journal of the History of Astronomy 33, 219 (2002).

Коперник Н. О вращениях небесных сфер / Пер. с лат. И. Н. Веселовского. – М.: Наука, 1964. С. 13.

Уайт Э. Д. Борьба религии с наукой / Пер. Д. Л. Вейса; Предисл. А. Б. Рановича. – 2‑е изд. – М.: ГАИЗ, 1936.

Абзац процитирован по: Lindberg и Numbers, «Beyond War and Peace», и T. Kuhn, The Copernican Revolution (Harvard University Press, Cambridge, Mass., 1957), p. 191. Кун (Kuhn) воспользовался White, A History of the Warfare of Science with Theology. The German original is Sämtliche Schriften, ed. J. G. Walch (J. J. Gebauer, Halle, 1743), Vol. 22, p. 2260.

Здесь Лютер упоминает Библию, «Книга Иисуса Навина» 10:12.

Из английского перевода Rosen,Nicolas Copernicus On the Revolutions.

Цит. по: R. Christianson, Tycho’s Island (Cambridge University Press, Cambridge, 2000), p. 17.

См.: Edward Rosen, The Dissolution of the Solid Celestial Spheres // Journal of the History of Ideas 46, 13 (1985).

Об этих перипетиях см.: C. Schofield, «The Tychonic and Semi‑Tychonic World Systems», в Planetary Astronomy from the Renaissance to the Rise of Astrophysics – Part A: Tycho Brahe to Newton, ed. R. Taton и C. Wilson

Существует 120 перестановок пяти разных предметов; любой из пяти может быть первым, любой из оставшихся четырех – вторым, любой из оставшихся – третьим и любой из последних двух – четвертым, оставляя одну возможность для пятого. Таким образом, количество способов разместить пять предметов в определенном порядке вычисляется так: 5 × 4 × 3 × 2 × 1 = 120. Но в задаче о соотношениях размеров сфер, вписанных в многогранники и описанных вокруг них, не все из пяти правильных многогранников отличаются. Это соотношение одинаково для куба и октаэдра, а также для икосаэдра и додекаэдра. Таким образом, два ряда правильных многогранников, которые могут отличаться только взаимными заменами куба и октаэдра или икосаэдра и додекаэдра, дают одну и ту же модель Солнечной системы. Следовательно, количество разных моделей составляет 120/(2 × 2) =30.

Например, если куб вписан во внутренний радиус сферы Сатурна и описан вокруг внешнего радиуса сферы Юпитера, тогда соотношение минимального и максимального расстояния от Сатурна до Солнца, которое, согласно Копернику, равно 1,586, должно равняться расстоянию от центра куба до любой из его вершин, деленному на расстояние от центра того же куба до любой из его граней, или √3=1.732, что на 9 % больше.

S. Weinberg, «Anthropic Bound on the Cosmological Constant» // Physical Review Letters 59, 2607 (1987); H. Martel, P. Shapiro, и S. Weinberg, «Likely Values of the Cosmological Constant» // Astrophysical Journal 492, 29 (1998).

Движение Марса является идеальной проверкой для теории движения планет. В отличие от Меркурия или Венеры, Марс виден, когда он находится высоко на ночном небе, что облегчает наблюдения. В любой заданный отрезок времени он проходит намного больший путь по орбите, чем Юпитер или Сатурн. Также его орбита отклоняется от круговой формы больше, чем орбиты всех остальных крупных планет, за исключением Меркурия (который не виден вдали от Солнца, что усложняет его наблюдения), поэтому отклонения от кругового движения с постоянной скоростью для Марса заметны гораздо сильнее, чем для остальных планет.

Основной эффект от эллиптической формы орбит планет состоит по большей части не в самой эллиптичности, а в том, что Солнце находится в фокусе эллипса, а не в центре. Если быть точным, то расстояние между одним из фокусов и центром эллипса пропорционально эксцентриситету, в то время как диапазон изменения расстояний от любой точки на эллипсе до заданного фокуса пропорционален квадрату эксцентриситета, то есть маленький эксцентриситет делает эту разницу расстояний совсем небольшой. Например, для эксцентриситета 0,1 (близкого к эксцентриситету орбиты Марса) наименьшее расстояние от планеты до Солнца всего на 0,5 % меньше, чем наибольшее расстояние. С другой стороны, расстояние от Солнца до центра этой орбиты составляет 10 % среднего радиуса орбиты. (Предлагаю читателю самостоятельно проверить это утверждение автора. – Прим. науч. ред. )

J. R. Voelkel and O. Gingerich, Giovanni Antonio Magini's «Keplerian» Tables of 1614 and Their Implications for the Reception of Keplerian Astronomy in the Seventeenth Century, Journal for the History of Astronomy 32, 237 (2001).

Имеется в виду Жюль Сезар (Юлий Цезарь) Скалигер, страстный защитник Аристотеля и оппонент Коперника.

По кн.: Robert S. Westfall in The Construction of Modern Science – Mechanism and Mechanics (Cambridge University Press, Cambridge, UK, 1977). P. 10.

William H. Donahue, in Johannes Kepler – New Astronomy (Cambridge University Press, Cambridge, 1992), p. 65.

Johannes Kepler, Epitome of Copernican Astronomy and Harmonies of the World, trans. Charles Glenn Wallis (Prometheus, Amherst, N.Y., 1995), p. 180.

Дальнейший текст показывает, что под средним расстоянием планеты от Солнца Кеплер имел в виду не расстояние, усредненное по времени, по полному периоду обращения планеты, а среднее арифметическое минимального и максимального расстояний между Солнцем и планетой. Как демонстрируется в техническом замечании 18, минимальное и максимальное расстояние от Солнца до планеты равняются, соответственно, (1 – e ) a и (1 + e ) a, где e – эксцентриситет, и a – половина длинной оси эллипса (или, иначе, большая полуось). Отсюда среднее расстояние равняется просто a . Как доказывается далее в техническом замечании 18, эта же величина является средним расстоянием между Солнцем и планетой, если усреднять по расстоянию, проходимому планетой вдоль своей орбиты.

Цит. по: Owen Gingerich, Tribute to Galileo in Padua, International Symposium a cura dell' Universita di Padova, 2–6 Dec. 1992, Vol. 4 (Edizioni LINT, Trieste, 1995).

[12]Полента – итальянская каша из кукурузной муки. – Прим. пер.

Фокусное расстояние – это длина, которая характеризует оптические свойства линзы. Для выпуклых линз это расстояние позади линзы, на котором проходящие через линзу по параллельным направлениям лучи сходятся в одной точке. Для вогнутых линз фокусное расстояние – это расстояние позади линзы, на котором лучи собрались бы в одной точке, если бы линзы не было, в предположении, что линза превращает эти лучи в параллельные. Фокусное расстояние зависит от кривизны поверхностей линзы и от соотношения скоростей света в воздухе и в стекле (см. техническое замечание 22).

[13]Дож – титул главы государства в республиках Генуэзской и Венецианской. – Прим. ред.

Галилео Галилей. Избранные труды: в 2 т. Т. 1 / Пер. и прим. И. Н. Веселовского. – М.: Наука, 1964. С. 14.

Угловой размер планет достаточно велик, чтобы лучи с различных точек их дисков, направленные в глаз наблюдателя, проходя сквозь земную атмосферу, располагались на расстояниях, превышающих размер обычных атмосферных возмущений. Таким образом, эффекты нескольких различных возмущений на пути лучей света от отдельных точек диска планеты взаимно не коррелируют и вследствие этого чаще взаимно компенсируются, а не усиливаются. Поэтому мы не видим планеты мерцающими.

Галилео расстроился бы, если бы узнал, что именно эти названия прижились в дальнейшем и употребляются в наше время. Так спутники Юпитера назвал в 1614 г. Симон Майр, немецкий астроном, который оспаривал первенство Галилея в их открытии.

Галилео Галилей. Рассуждение о телах, пребывающих в воде// Избранные труды: в 2 т. Т. 2/Пер. и прим. И. Н. Веселовского. – М.: Наука, 1964. С. 39.

Предположительно, Галилей пользовался не часами, а ориентировался по видимому движению звезд. Поскольку звездам необходимо примерно 24 часа, чтобы совершить видимый оборот вокруг Земли на 360°, изменение положения звезды на один градус указывает на то, что прошла 1/360 часть этого времени, то есть 4 минуты.

[14]Один из телескопов Галилея достался Кеплеру случайно и на короткое время, с 29 августа по 9 сентября 1610 г. См.: Шмутцер Э., Шютц В. Галилео Галилей. – М.: Мир, 1987. – С. 47. – Прим. науч. ред.

Современный английский перевод книги: Thomas Salusbury Galileo, Discourse on Bodies in Water, intr. and comm. Stillman Drake.

Подробности см.: J. L. Heilbron, Galileo (Oxford University Press, Oxford, 2010).

Галилео Галилей. Пробирных дел мастер. – М.: Наука, 1987.

Русский пер. цит. по: Кузнецов Б. Г. Галилео Галилей. – М.: Наука, 1964. С. 117.

Перевод письма на английский см.: Drake, Discoveries and Opinions of Galileo, pp. 175–216.

[15]Автор цитирует только первую половину заключения квалификаторов инквизиции, касающегося покоя Солнца в центре Вселенной. – Прим. ред.

Дмитриев И.С. Упрямый Галилей. – М.: Новое литературное обозрение, 2018. С. 145.

[16]«А все‑таки она вертится!»

Письма Марии отцу к счастью сохранились. См.: Dava Sobel, Galileo's Daughter (Walker, New York, 1999). Увы, письма Галилея к дочерям утрачены.

См.: Annibale Fantoli, Galileo – For Copernicanism and for the Church, 2nd ed., trans. G. V. Coyne (University of Notre Dame Press, South Bend, Ind., 1996); Maurice A. Finocchiaro, Retrying Galileo, 1633–1992 (University of California Press, Berkeley and Los Angeles, 2005).

Цит. по: Drake, Galileo, p. 90.

Цит. по: Gingerich, Tribute to Galileo, p. 343.

Я выступил с докладом на эту тему на том же заседании в Падуя, где Кюн говорил по поводу Аристотеля (цитируется в гл. 4) и где Гингерич, слова которого я привожу здесь, говорил о Галилее. См.: S. Weinberg, в L'Anno Galileiano (Edizioni LINT, Trieste, 1995), p. 129.

См.: G. E. R. Lloyd, Proceedings of the Cambridge Philosophical Society, N.S. 10, 50 (1972), напечатано в: Methods and Problems in Greek Science (Cambridge University Press, Cambridge, 1991).

Галилео Галилей. Беседы и математические доказательства двух новых наук // Избранные труды: в 2 т. Т. 2/Сост. У. И. Франкфурт; пер. С. Я. Долгова. – М.: Наука, 1964. С. 166.

Это справедливо только для малых колебаний маятника, хотя Галилей не упоминал об этом ограничении. Более того, он говорит об изохронизме при отклонениях маятника на 50°–60°, как и при колебаниях с меньшей амплитудой, что говорит о том, что он на самом деле не производил тех экспериментов с маятником, о которых рассказывает.

Если говорить буквально, это значило, что любое брошенное тело никогда бы не упало, поскольку, обладая нулевой начальной скоростью в первое бесконечно малое мгновение, оно никуда бы не двинулось. А поскольку скорость пропорциональна пройденному расстоянию, она равнялась бы нулю. Возможно, о скорости, пропорциональной пройденному расстоянию, имеет смысл говорить только после короткого первоначального периода ускорения.

Один из аргументов Галилея является ошибочным, потому что относится к средней скорости за период времени, а не к скорости, которая достигается в конце интервала.

Это показано в техническом замечании 25. Там объясняется, что, хотя Галилей об этом и не знал, но скорость шара, катящегося по плоскости, не равна скорости тела, свободно падающего с того же расстояния по вертикали, потому что часть энергии, получаемой от вертикального падения, уходит во вращение шара. Но эти скорости будут пропорциональны, так что заключение Галилея о том, что скорость падающего тела пропорциональна затраченному времени, качественно не изменится, если мы примем во внимание вращение шара.

См.: Stillman Drake, Galileo (Oxford University Press, Oxford, 1980), p. 33.

T. B. Settle, An Experiment in the History of Science // Science 133, 19 (1961).

Это заключение Дрейка можно найти в примечании к с.259 книги: Galileo Galilei, Dialogue Concerning the Two Chief World Systems: Ptolemaic and Copernican, trans. Stillman Drake (Modern Library, New York, 2001).

См.: Stillman Drake, Galileo at Work – His Scientific Biography (University of Chicago Press, Chicago, Ill., 1978), pp. 128–32; A. J. Hahn, The Pendulum Swings Again: A Mathematical Reassessment of Galileo's Experiments with Inclined Planes // Archive for the History of the Exact Sciences 56, 339 (2002), с репродукцией на p. 344.

Carlo M. Cipolla, Clocks and Culture 1300–1700 (W. W. Norton, New York, 1978), pp. 59, 138.

Гюйгенс Х. Три мемуара по механике. – М.: Изд. АН СССР, 1951. С. 201.

Детальное описание измерений см.: Alexandre Koyré, Proceedings of the American Philosophical Society 97, 222 (1953) и 45, 329 (1955). Также см.: Christopher M. Graney, Anatomy of a Fall: Giovanni Battista Riccioli and the Story of g // Physics Today, Sept. 2012, pp. 36–40.

По поводу расногласий относительно законов сохранения см.: G. E. Smith, The Vis‑Viva Dispute: A Controversy at the Dawn of Mathematics // Physics Today, Oct. 2006, p. 31.

Гюйгенс Х. Трактат о свете, в котором объяснены причины того, что с ним происходит при отражении и преломлении, в частности при странном преломлении исландского кристалла/Пер. с фр., под ред. и с прим. В. К. Фредерикса. – 2‑е изд. – М.: Книжный дом «ЛИБРОКОМ», 2010. С. 6−7.

Цит. по: Steven Shapin in The Scientific Revolution (University of Chicago Press, Chicago, Ill., 1996), p. 105.

[17]В русской научной традиции – 760 мм ртутного столба. – Прим. пер.

Ibid, p. 185.

См. статью «Leonardo» // Dictionary of Scientific Biography, Charles Coulston Gillespie (Scribner, New York, 1970), Vol. 8, pp. 192–245.

[18]Так во Франции XVII в. называли дворянство, приобретенное на государственной службе. – Прим. пер.

Декарт Р. Сочинения: в 2 т. Т. 1 / Сост., ред., вступ. ст. В. В. Соколова. – М.: Мысль, 1989. С. 235.

Декарт сравнивал свет с жестким прутом. Когда толкают один его конец, немедленно начинает двигаться и другой. Насчет прутьев он тоже ошибался, хотя и по причинам, в то время неизвестным. Когда толкают один конец прута, с другим ничего не происходит, пока волна сжатия (подобно звуковой волне) не пройдет с одного конца прута на другой. Скорость этой волны возрастает в зависимости от жесткости прута, но Специальная теория относительности Эйнштейна не допускает существования идеально жестких предметов; ни одна волна не может достигнуть скорости, превышающей скорость света. Использование Декартом такого рода сравнения обсуждается Питером Галисоном в статье «Декартовы сравнения: от невидимого к видимому» (Galison P. Descartes comparisons: From the invisible to the visible // Isis. 1984. Vol. 75. P. 311–326).

Вольтер. Философские сочинения / Пер. с фр. С. Я. Шейнман‑Топштейн. – М: Наука, 1988. С. 134.

Декарт Р. Сочинения. Т. 1. С. 250.

Напомним, что синус угла – это длина катета, противолежащего данному углу в прямоугольном треугольнике, деленная на длину гипотенузы этого треугольника. Он возрастает при увеличении угла от 0° до 90°, сначала пропорционально самому углу, когда его значения небольшие, а затем растет медленнее.

Есть мнение, что аналогия с теннисными мячиками подходит для теории света Декарта, если их сравнить с мельчайшими корпускулами, пронизывающими пространство. См.: John A. Schuster, Descartes Opticien – The Construction of the Law of Refraction and the Manufacture of Its Physical Rationales, 1618–1629, в: Descartes' Natural Philosophy, eds. S. Graukroger, J. Schuster, and J. Sutton (Routledge, London and New York, 2000), pp. 258–312.

Аристотель. Сочинения. Т. 3. C. 518.

Это делается путем нахождения значения отношения b /R , где ничтожно малые изменения значения b не оказывают влияния на φ, поэтому при таких значениях φ график зависимости φ от b /R в этом месте будет плоским. Это и есть значение b /R , при котором φ достигает максимальной величины (как и любая гладкая кривая, график зависимости φ от b /R , который поднимается до своего максимума, а затем снижается, будет горизонтален в точке максимума. Точка, где кривая не плоская, не может быть максимумом, поскольку если в какой‑либо точке кривая растет вправо или влево, то будут точки справа или слева, где значение функции будет выше). Значение φ в промежутке, где кривая зависимости φ от b /R почти плоская, изменяется очень медленно, если мы сдвигаем аргумент b /R , поэтому существует относительно большое количество лучей со значением φ в этом диапазоне.

Декарт Р. Сочинения. Т. 1. С. 297.

См. Peter Dear, Revolutionizing the Sciences – European Knowledge and Its Ambitions, 1500–1700, 2nd ed. (Princeton University Press, Princeton, N.J., and Oxford, 2009), Chapter 8.

L. Laudan, The Clock Metaphor and Probabilism: The Impact of Descartes on English Methodological Thought // Annals of Science 22, 73 (1966). Contrary conclusions were reached in G. A. J. Rogers, Descartes and the Method of English Science // Annals of Science 29, 237 (1972).

Richard Watson, Cogito Ergo Sum – The Life of René Descartes (David R. Godine, Boston, Mass., 2002).

Когда ему было за пятьдесят, Ньютон нанял в качестве домработницы дочь своей сводной сестры красавицу Катрин Бартон. Несмотря на то что они были близкими друзьями, романтических отношений между ними не было. Вольтер, который был в Англии, когда Ньютон умер, сообщил, что врач Ньютона и «хирург, в руках которого он умер» подтвердили, что у Ньютона никогда не было интимных отношений с женщинами. См.: Вольтер. Философские сочинения. С. 133. Вольтер нигде не указывает, как доктор и хирург узнали об этом.

Из речи «Ньютон, Человек», которую Кейнс готовил для собрания Королевского общества в 1946 г. За три месяца до собрания Кейнс скончался, и речь была представлена его братом.

См. D. T. Whiteside, ed., General Introduction to Vol. 20, The Mathematical Papers of Isaac Newton (Cambridge University Press, Cambridge, 1968), pp. xi – xii.

Вполне сопоставимые усилия Ньютон потратил на эксперименты в алхимии, которую вполне можно было назвать химией, поскольку в те времена разница между ними была незначительной. Как я уже отмечал в связи с Джабир ибн Хайяном в главе 9, до конца XVIII в. не существовало химической теории, которая отвергала бы алхимические превращения, такие как трансформация недрагоценных металлов в золото. Таким образом, хотя работа Ньютона по алхимии не была антинаучной, она не содержала ничего важного.

При прохождении света через плоское стекло разделения на разные цвета не произойдет, потому что лучи каждого цвета преломляются под очень маленьким углом и возвращаются на первоначальные направления движения, покидая стекло. Поскольку грани призмы не параллельны, лучи света разных цветов, проходя сквозь призму, преломляются по‑разному и, достигая поверхности призмы, выходят из нее под углами, не равными углам преломления или входа, поэтому, когда эти лучи покидают призму, появляются разные цвета.

Это натуральный логарифм от 1 + х , то есть степень, в которую постоянная e = 2,71828… должна быть возведена, чтобы в результате получилось 1 + х. Причина такой особенности этого определения в том, что натуральные логарифмы по своим свойствам гораздо проще десятичных логарифмов, где основанием вместо е берется число 10. Например, формула Ньютона показывает, что натуральный логарифм 2 может быть представлен в виде числового ряда 1 − 1/2 + 1/3 − 1/4 +…, тогда как формула десятичного логарифма 2 гораздо более сложна.

Из‑за пренебрежения членами 3to ² и o³ может показаться, что эти расчеты являются только приблизительными, но это неверно. В XIX в. математики научились обходиться без достаточно расплывчатого понятия бесконечно малой величины о и вместо этого стали говорить о точно определенных пределах: скорость – это число, к которому можно приближать функцию [D (t+o) – D (t)] / o настолько, насколько малым нам удобно брать значение o . Как мы увидим далее, Ньютон позже перешел от бесконечно малых величин к современной идее пределов.

D. T. Whiteside. Op. cit. Vol. 3. Pp. 6–7.

См., напр.: Richard S. Westfall, Never of Rest – A Biography of Isaac Newton (Cambridge University Press, Cambridge, 1980). Chapter 14.

Peter Galison, How Experiments End (University of Chicago Press, Chicago, Ill., 1987).

Цит. по: Richard S. Op. cit. P. 143.

Три закона планетарного движения Кеплера не всеми принимались до Ньютона, хотя первый закон о том, что орбиты планет являются эллипсами, в фокусе которых находится Солнце, был широко распространен. Именно выведение Ньютоном тех же законов в своих «Началах» привело к их всеобщему признанию.

Первое достаточно точное измерение длины окружности Земли было сделано примерно в 1669 г. Жан‑Феликсом Пикаром (1620–1682). В