Вывод закона преломления света на основе принципа наименьшего времени

Герон Александрийский сформулировал закон отражения световых лучей так: угол наклона отраженного луча равен углу наклона падающего. Он исходил из предположения, что путь луча света от объекта к поверхности зеркала и затем к наблюдателю должен быть как можно короче. Точно так же он мог положить в основу и правило о том, что путь луча должен занимать самое короткое время, поскольку время, нужное свету, чтобы преодолеть заданное расстояние, равно частному от деления этого расстояния на скорость света, а в процессе отражения скорость света не изменяется. Однако, когда наблюдается явление преломления, свет проходит сквозь границу двух сред (например, воздуха и стекла), в которых его скорость различна, и приходится рассматривать разницу между понятиями кратчайшего пути и наименьшего времени. Один только факт, что луч света меняет направление на границе сред, говорит о том, что преломленный свет не следует по самому короткому пути в этом случае – прямой линии. Зато, как доказал Ферма, истинный закон преломления света можно вывести, предполагая, что свет стремится затратить как можно меньше времени, чтобы достигнуть цели.

Чтобы получить такой результат, допустим, что свет проходит от точки P_A в среде A , где скорость света равна v_A , к точке P_B в среде B , в которой скорость света равна v_B . Для простоты описания задачи предположим, что поверхность границы раздела сред горизонтальна. Обозначим углы между направлениями лучей света в первой и второй средах и вертикалью i и r соответственно. Если точки P_A и P_B находятся на соответствующих вертикальных расстояниях d_A и b_B от границы раздела, то горизонтальные промежутки между этими точками и той точкой, где луч пересекает поверхность, равны, соответственно, d_A tg i и d_B tg r , где символ «tg» обозначает функцию тангенса угла, отношения длины противолежащего катета к длине прилежащего катета в прямоугольном треугольнике (см. рис. 21). Хотя мы не фиксируем заранее эти два расстояния, их сумма нам известна – это горизонтальное расстояние L между точками P_A и P_B :

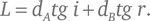
Чтобы вычислить время t , которое требуется свету для преодоления пути из P_A в P_B , обратим внимание, что пройденное им расстояние в средах A и B равняется d_A /cos i и d_B /cos r , соответственно, где «cos» – обозначение функции косинуса угла, отношения длины прилежащего к углу катета к гипотенузе в прямоугольном треугольнике. Время равно расстоянию, деленному на скорость, поэтому полное время будет таково:

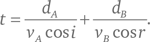
Нам необходимо найти общую зависимость между углами i и r (не включающую параметры L, d_A или d_B ), которая удовлетворяет условиям: угол i таков, что общее время t минимально, а величина r связана с величиной i таким образом, что L остается фиксированным. Для этого введем в рассмотрение δi , ничтожно малое изменение δ (дельта) угла падения луча i . Так как горизонтальное расстояние между P_A и P_B постоянно, при изменении угла i на δi угол преломления r также должен измениться, допустим, на величину δr , при условии сохранения расстояния L . Также в точке минимума функции времени t в зависимости от угла i график этой функции должен иметь горизонтальный участок, поскольку, если t в какой‑то точке увеличивается или уменьшается, значит, его минимальное значение соответствует какому‑то другому значению аргумента i , где сама функция t меньше. Это означает, что изменение t , вызванное ничтожно малым изменением угла δi , обращается в ноль, по крайней мере с точностью до первого порядка величины δi .

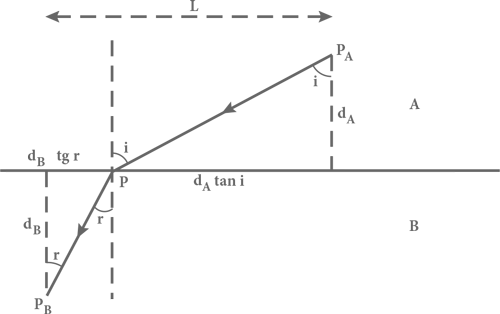
Рис. 21. Путь луча света, испытывающего преломление. Горизонтальной линией отмечена граница двух прозрачных сред A и B , в которых свет имеет различные скорости v_A и v_B . Углы i и r измеряются между направлениями светового луча и вертикальной штриховой линией, обозначающей перпендикуляр к границе раздела сред. Сплошная линия со стрелками отмечает путь следования луча из точки P_A в среде A до точки P на границе раздела сред и затем до точки P_B в толще среды B .

Поэтому, чтобы найти путь, для прохождения которого свету требуется наименьшее время, мы можем ввести условие: при одновременном изменении i и r изменения δL и δt должны оставаться нулевыми с точностью до первого порядка величин δi и δr .

Чтобы удовлетворить ему, нам необходимо взять пару стандартных формул дифференциального исчисления для бесконечно малых изменений значений функций δ tg θ (тета) и δ (1/cos θ), которые получаются, когда мы изменяем угол‑аргумент θ на бесконечно малую величину δθ:

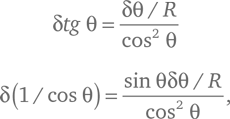
где R = 360°/2π = 57,293…° в случае, когда θ измеряется в градусах (это угол размером в один радиан. При измерении углов в радианах R = 1). По этим формулам мы находим изменения L и t в случае, когда мы меняем углы i и r на бесконечно малые величины δi и δr :

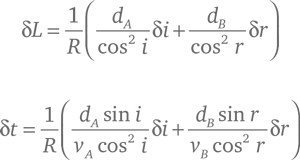
Заданное условие δL = 0 говорит нам, что

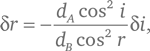
поэтому:

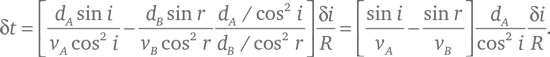
Полученное выражение приравнивается к нулю, если удовлетворяется равенство

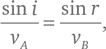
или, иначе говоря,

причем показатель преломления n получается из отношения скоростей, не зависящего от углов:

n = v_A / v_B.

Это и есть истинный закон преломления света, в котором формула для показателя преломления n верна.

Теория радуги

Пусть луч света проникает в сферическую каплю дождя в некоторой точке P на ее поверхности, образуя угол i с нормалью (перпендикуляром) к ее поверхности в этой точке. Если бы преломления света не было, луч продолжал бы идти дальше сквозь каплю по прямой. В этом случае радиус, проведенный из центра капли C к точке Q , лежащей на этой прямой в том месте, где она наиболее близко пролегает к центру капли, образовывал бы с лучом прямой угол, поэтому треугольник PCQ был бы прямоугольным с гипотенузой, равной радиусу капли R , и углом при точке P , равным i (см. рис. 22а). Определим прицельный параметр b как расстояние наибольшего тесного сближения непреломленного луча с центром капли, то есть катетом CQ в этом треугольнике, который по правилам элементарной тригонометрии равен:

b = R sin i .

С точки зрения положения точки входа в каплю отдельные лучи света можно одинаково хорошо охарактеризовать присущим им отношением b /R , как делал Декарт, или же по значению угла падения i .

В силу явления преломления луч на самом деле войдет внутрь капли под углом r к перпендикуляру к поверхности, значение которого определяется законом преломления:

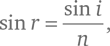
где n ≈ 4/3 – отношение скорости света в воздухе к скорости света в воде. Луч пересечет толщу капли и достигнет поверхности с обратной стороны в точке P’ . Поскольку расстояния между центром C и обеими точками P и P’ одинаковы и равны радиусу капли R , треугольник с вершинами C, P и P’ является равнобедренным, поэтому углы между направлением луча и перпендикулярами к поверхности в точках P и P’ должны быть одинаковы, то есть и тот и другой равны r . Часть света отразится в точке P’ от внутренней поверхности капли: по закону отражения угол между отраженным лучом и перпендикуляром к поверхности в ней будет опять же равен r . Затем отраженный луч снова пересечет толщу капли и достигнет ее передней поверхности в точке P’’ , снова образуя с поверхностью угол r .

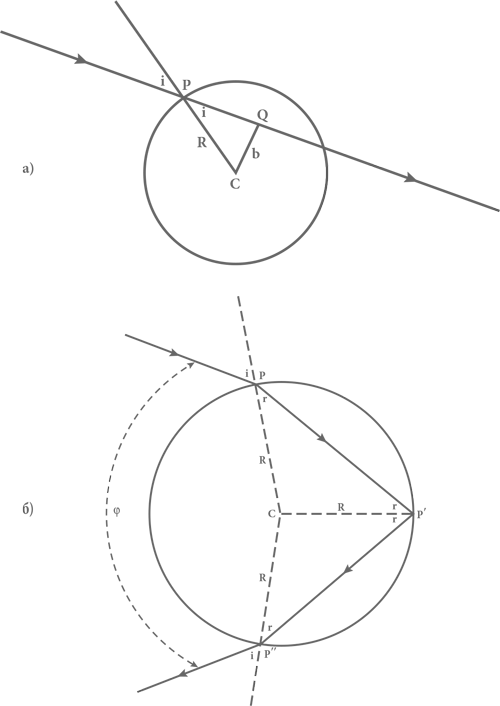
Рис. 22. Путь солнечного луча внутри сферической дождевой капли. Луч обозначен сплошными отрезками с указывающими направление стрелками: он входит внутрь капли в точке P под углом i к перпендикуляру к поверхности: а) путь луча, если бы явления преломления не было: луч в этом случае приближается к центру капли C в точке Q ; б) луч преломляется, входя в каплю в точке P , отражается от задней поверхности капли в точке P’ и снова подвергается преломлению в момент выхода из капли в точке P’’ . Пунктирные линии проведены из центра капли C к точкам контакта луча с поверхностью капли.

Часть света затем покидает каплю, и по закону преломления угол между выходящим наружу лучом и перпендикуляром к поверхности в точке P’’ будет равен исходному углу падения i (см. рис. 22 – здесь показана схема следования луча в плоскости, проходящей через падающий луч, центр капли и наблюдателя. Только те лучи, которые встречаются с каплей, находясь в этой плоскости, имеют возможность достигнуть наблюдателя).

По мере всей этой серии поворотов луч света отклонится в сторону центра капли на угол i – r дважды – в моменты входа в каплю и выхода из нее, и на угол 180° – 2r при отражении от ее задней поверхности, и значит, полный угол поворота луча составит:

2(i − r) + 180° − 2r = 180° − 4r + 2i.

Если бы луч возвращался из капли в направлении, точно противоположном тому, в котором вошел (это происходит в случае, когда i = r = 0), этот угол составил бы 180°, а начальное и конечное направления луча были бы параллельны, поэтому действительный угол φ между ними равен:

R − 2i.

Можно выразить r как функцию от i , вот так:

где для любого аргумента x функция arcsin x – это угол (обычно принимаемый в промежутке от –90° до +90°), синус которого равен x . Численный расчет для показателя n = 4/3, который нам встречается в главе 13, показывает, что φ возрастает от нуля при i = 0 до максимального значения при 42° и затем снижается примерно до 14° при i = 90°. График зависимости φ от i горизонтален в своей точке максимума, поэтому большая часть света выходит из капли, подвергаясь отклонению на полный угол, близкий к 42°.

Если мы посмотрим на облачное небо, повернувшись к солнечным лучам спиной, то увидим свет, приходящий к нам под углом 42° между нашим лучом зрения и световыми лучами от солнца. Совокупность этих направлений формирует дугу, которая для нас обычно поднимается в небо из одной точки горизонта и затем опускается к земле в другой. Поскольку коэффициент преломления n слегка варьируется в зависимости от цвета преломляемого луча, для лучей различного цвета углы отклонения φ тоже слегка отличаются, поэтому мы видим дугу, образованную чередованием полос разного цвета. Это и есть радуга.

Нетрудно вывести аналитическую формулу, дающую максимальное значение φ для любого коэффициента преломления n . Чтобы найти максимум φ, примем во внимание тот факт, что точке максимума соответствует такое значение угла падения i , при котором график зависимости φ от i горизонтален, а это означает, что ничтожно малое изменение δφ угла φ, происходящее вследствие ничтожно малого изменения δi угла i , равняется нулю с точностью до первого порядка величины δi . Чтобы использовать это условие, применим табличную формулу из курса дифференциального исчисления, согласно которой при ничтожно малом изменении δх аргумента x изменение arcsin x равно:

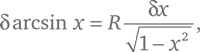
где, если arcsin x измеряется в градусах, R = 360°/2π . Таким образом, когда угол падения изменяется на величину δi , угол отклонения меняется на:

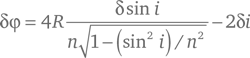
или, поскольку δ sin i = cos i δi /R ,

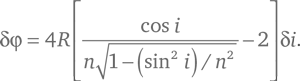
Таким образом, условие максимального значения φ таково, что:

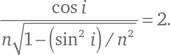
Возведя обе части в квадрат и используя правило cos²i = 1 − sin²i (которое является следствием из теоремы Пифагора), мы можем найти из этого выражения значение для sin i :

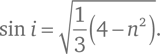
При этом значении угла падения угол φ максимален:

При n = 4/3 максимальный угол отклонения φ достигается при значении b /R = sin i = 0,86, для которого i = 59,4°, r = 40,2° и φ_max = 42,0°.