Центростремительное ускорение

Ускорение – это мера изменения скорости, но скорость любого тела характеризуется, с одной стороны, так называемым модулем скорости, то есть ее абсолютной величиной, с другой – направлением. Скорость тела, движущегося по окружности, постоянно меняет свое направление по мере поворота вокруг центра окружности, поэтому даже при постоянном модуле скорости оно движется с ускорением в сторону центра, которое называется центростремительным.

Давайте рассчитаем центростремительное ускорение для тела, которое обращается по окружности радиусом r с постоянной скоростью v . За короткий промежуток времени между моментами t ₁ и t ₂ тело переместится вдоль окружности на небольшое расстояние v Δt , где Δt равняется t ₂− t ₁, а радиус‑вектор (стрелка, указывающая из центра окружности на тело) повернется на малый угол Δθ. Вектор скорости (стрелка, направленная в ту сторону, куда в данный момент движется тело, с длиной, пропорциональной текущему значению скорости) всегда направлен по касательной к окружности и, значит, перпендикулярно к радиус‑вектору, так что если направление радиус‑вектора меняется на угол Δθ, то и направление вектора скорости изменится на тот же самый малый угол. Таким образом, мы получаем два треугольника: сторонами первого являются радиус‑векторы тела в моменты t ₁ и t ₂, а также хорда, соединяющая позиции тела в эти два момента. Стороны второго треугольника – векторы скорости в моменты t ₁ и t ₂, а также изменение скорости Δv , произошедшее за этот промежуток времени (см. рис. 24). Для небольших значений углов Δθ можно не учитывать разницу в длине хорды и дуги, соединяющих две последовательные позиции тела в моменты t ₁ и t ₂, поэтому можно считать длину хорды равной v Δt .

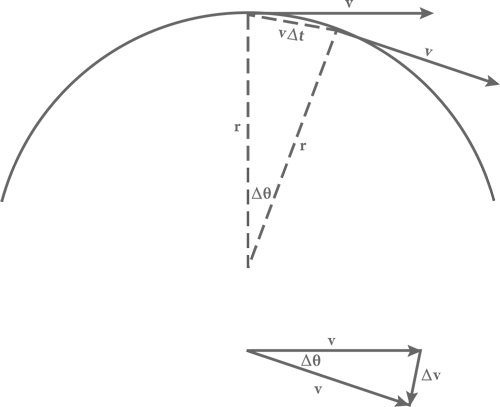
Рис. 24. Расчет центростремительного ускорения. Вверху: векторы скорости тела, движущегося по окружности, в два различных момента времени, разделенных небольшим интервалом Δt . Внизу: те же два вектора скорости, совмещенные в треугольник, короткая сторона которого равна изменению скорости за тот же отрезок времени.

Мы видим, что эти два треугольника подобны (то есть они отличаются размерами, но не отношением сторон друг к другу), поскольку оба являются равнобедренными (у них по две одинаковые стороны), и между сторонами одинаковой длины один и тот же небольшой угол Δθ. Поэтому отношения короткой и длинной сторон в обоих треугольниках должны быть взаимно равны. То есть

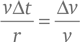
и, значит,

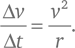
Это – выведенная Гюйгенсом формула центростремительного ускорения.