Вариационные основы МКЭ
При решении многих задач статики, динамики и устойчивости сооружений определяется их полная потенциальная энергия U:
U = W – V. (1)
Здесь W – работа внешних сил, V – работа внутренних сил. Обычно все они представляются в виде функций, зависящих от перемещений, деформаций, напряжений элементов расчетной модели сооружения.
Исследование этого выражения позволяет выявить важные законы механики, называемые принципами. Например, в теоретической механике известен принцип Лагранжа-Дирихле: для того чтобы механическая система находилась в равновесии, ее полная потенциальная энергия должна быть постоянной. Из этого принципа следует, что приращение полной потенциальной энергии системы, находящейся в равновесии, должно равняться нулю:
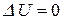 .
.
Вычисление приращения функции обычно заменяется вычислением его приближенного значения − дифференциала. В этом случае получается вариационное уравнение Лагранжа
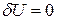 ,
,
где символ 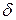 означает вариацию, вычисление которого схоже с вычислением дифференциала функции. Это уравнение позволяет свести задачу определения НДС сооружения к отысканию экстремума полной потенциальной энергии.
означает вариацию, вычисление которого схоже с вычислением дифференциала функции. Это уравнение позволяет свести задачу определения НДС сооружения к отысканию экстремума полной потенциальной энергии.
С учетом (1) вариационное уравнение Лагранжа принимает вид
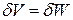 .
.
Оно формулируется как принцип Лагранжа: вариация работы внутренних сил равна вариации работы внешних сил.
Принцип Лагранжа используется для сведения континуальной задачи расчета сооружений к дискретной задаче путем аппроксимации (приближенного определения) непрерывных полей перемещений, деформаций, напряжений внутри конечного элемента по его узловым перемещениям.
В строительной механике используются и другие вариационные принципы, аналогичные принципу Лагранжа, такие как принципы Кастильяно, Рейсснера, Ху-Вашицу и др. Однако мы воспользуемся только вариационным принципом Лагранжа как основой варианта МКЭ в форме метода перемещений.
Аппроксимация КЭ
Имея КЭ разного типа, при выборе конечно-элементной модели сооружения можно вводить узлы с разным числом степеней свободы. Например, в плоской системе могут рассматриваться узлы как с тремя степенями свободы (рис. 14.2 а), так и с двумя (рис. 14.2 б) или даже с одной степенью свободы. В первом случае учитываются два линейных (поступательных) и одно угловое перемещение узла, во втором – два линейных перемещения, а в третьем − лишь одно поступательное перемещение. В пространственной системе узлы могут иметь шесть (рис. 14.2 в) или три степени свободы (рис. 14.2 г).
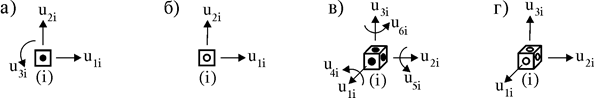
Рис. 14.2
Для упорядочения степеней свободы и соответствующих перемещений узлов КЭ все они нумеруются в определенном порядке и собираются в общий вектор перемещений u.
Чтобы воспользоваться принципом Лагранжа, вводятся так называемые координатные функции, аппроксимирующие непрерывное поле перемещений внутри КЭ через перемещения ее узлов:
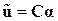 .
.
Здесь 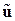 – вектор перемещений внутренних точек КЭ,C– матрица координатных функций,
– вектор перемещений внутренних точек КЭ,C– матрица координатных функций, 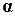 – вектор коэффициентов. Элементы матрицы C выбираются в виде полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число членов, то такой КЭ называется симплекс-элементом. При учете большего числа членов полинома КЭ называется комплекс-элементом.
– вектор коэффициентов. Элементы матрицы C выбираются в виде полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число членов, то такой КЭ называется симплекс-элементом. При учете большего числа членов полинома КЭ называется комплекс-элементом.
В качестве простейшего примера рассмотрим ферменный КЭ с узлами i и j (рис. 14.3 а) в местной системе координат 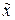 . Его узлы имеют по одной поступательной степени свободы по оси
. Его узлы имеют по одной поступательной степени свободы по оси 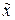 и соответствующие им узловые перемещения
и соответствующие им узловые перемещения 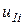 и
и 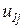 . Допустим, что в узлах КЭ приложены силы
. Допустим, что в узлах КЭ приложены силы 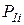 и
и 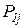 (рис. 14.3 б).
(рис. 14.3 б).
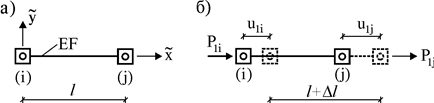
Рис. 14.3
Перемещения внутренних точек 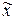 элемента будем аппроксимировать полиномом первой степени
элемента будем аппроксимировать полиномом первой степени
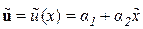 .
.
Запишем его в матричной форме:
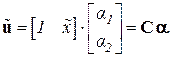 ,
,
где 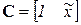 называется матрицей координатных функций, а
называется матрицей координатных функций, а 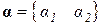 является вектором неизвестных коэффициентов.
является вектором неизвестных коэффициентов.
Подставив 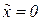 и
и 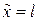 в наш полином, получим два равенства:
в наш полином, получим два равенства:
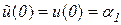 ,
, 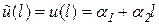 .
.
С другой стороны, 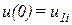 и
и 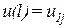 (рис. 14.3 б). Учитывая их, предыдущие равенства перепишем так:
(рис. 14.3 б). Учитывая их, предыдущие равенства перепишем так:
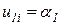 ,
,
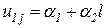 .
.
Тогда их можно записать в матричной форме
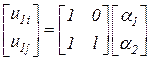
и представить как матричное уравнение
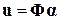 ,
,
связывающее вектор узловых перемещений 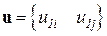 и вектор координат
и вектор координат 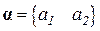 через представленную выше матрицу
через представленную выше матрицу 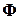 .
.
Определим вектор 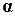 :
:
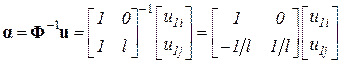 .
.
Тогда
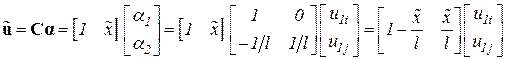
или
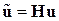 .
.
Входящая сюда матрица H 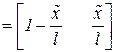 называется матрицей форм. Она позволяет аппроксимировать поле перемещений внутренних точек КЭ через перемещения узлов.
называется матрицей форм. Она позволяет аппроксимировать поле перемещений внутренних точек КЭ через перемещения узлов.
По аналогии с перемещениями поле внутренних усилий 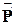 в КЭ можно аппроксимировать через вектор узловых сил
в КЭ можно аппроксимировать через вектор узловых сил 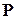 по формуле
по формуле
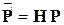 .
.
Например, для рассмотренного КЭ имеем
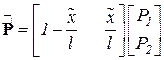 .
.
Дата добавления: 2016-01-29; просмотров: 1360;
