РАСЧЕТ СООРУЖЕНИЙ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Современная вычислительная техника позволяет проводить расчеты сооружений с более подробным описанием их внутренней структуры и с более точным учетом действующих нагрузок. Для этого разработаны специальные методы расчета, среди которых наибольшее распространение получил метод конечных элементов (МКЭ).

Понятие о методе конечных элементов

Метод конечных элементов – это метод расчета сооружений, основанный на рассмотрении сооружения как совокупности типовых элементов, называемых конечными элементами (КЭ).

В дискретном методе мы рассмотрели три типовых стержневых элементов, которые используются и в МКЭ как конечные элементы. Например, элемент 3-его типа в МКЭ называется ферменным (рис. 14.1 а), а 1-го типа – плоским стержневым конечным элементом (рис. 14.1 б). При расчете пространственных рам используется КЭ бруса (рис. 14.1 в). В расчетах плоских тел (плит или пластин) используются треугольный (рис. 14.1 г) или четырехугольный (рис. 14.1 д) конечные элементы. При расчете пространственных сооружений могут использоваться призменный КЭ (рис. 14.1 е) или тетраэдальный КЭ (рис. 14.1 ж) и др. Для расчета различных сооружений разработано множество других КЭ.

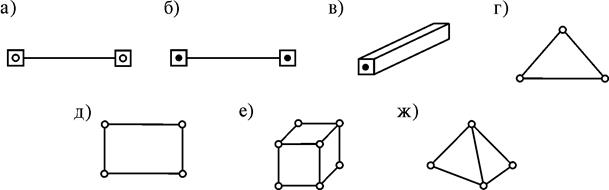
Рис. 14.1

МКЭ – дискретный метод. В этом методе сооружение делится на определенное число КЭ, соединенных между собой в узлах конечно-элементной модели. А нагрузка, действующая на сооружение, переносится в узлы. Это позволяет определять НДС сооружения через узловые усилия и перемещения конечно-элементной модели.

Как мы знаем, можно выбирать разные расчетные схемы сооружения. Но и в пределах одной расчетной схемы можно выбирать разные расчетные модели по МКЭ, потому что сооружение можно разбить не только на разное количество однотипных КЭ, но и представить его как комбинацию различных типов КЭ. С другой стороны, при расчете сооружения могут быть реализованы различные варианты МКЭ в формах метода сил, метода перемещений и смешанного метода. В настоящее время широкое распространение получил МКЭ в форме метода перемещений.