Переход к общей системе координат
Каждый КЭ в МКЭ вначале рассматривается в местной системе координат. Затем осуществляется переход к глобальной (общей) системе координат. Рассмотрим порядок такого перехода.
Пусть некоторый узел i в местной системе координат 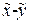 имеет перемещения
имеет перемещения 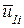 ,
,  ,
, 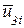 , которые следует преобразовать в перемещения узла
, которые следует преобразовать в перемещения узла 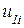 ,
, 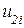 ,
, 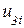 в общей системе координат x-y (рис. 15.2 а).
в общей системе координат x-y (рис. 15.2 а).
Поворот координатных осей осуществляется с помощью матрицы преобразования координат. Для плоской системы она имеет вид
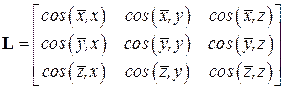 .
.
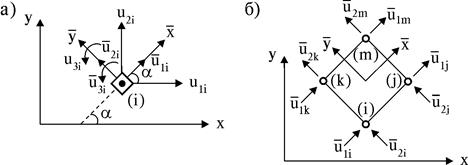
Рис. 15.2
Если координатные системы ортогональны и поворот осуществляется на угол a, то
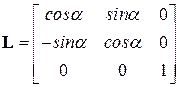 .
.
Для шарнирного узла с двумя степенями свободы
 . (1)
. (1)
Эти матрицы позволяют использовать матрицы и вектора геометрических и жесткостных характеристик КЭ, полученных в местной системе координат, для получения соответствующих характеристик КЭ в общей системе координат. Например, преобразование вектора координат прямоугольного КЭ с четырьмя шарнирными узлами i-j-k-m (рис. 15.2 б), рассматриваемогов местной системе координат 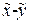 , в общую систему координат x-y осуществляет матрица
, в общую систему координат x-y осуществляет матрица
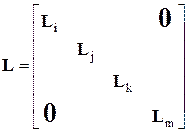 .
.
Блоки  этой матрицы имеют вид (1). Имея матрицу жесткости КЭ
этой матрицы имеют вид (1). Имея матрицу жесткости КЭ 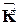 в местной системе координат, можно определять ее матрицу жесткости в общей системе координат по формуле
в местной системе координат, можно определять ее матрицу жесткости в общей системе координат по формуле
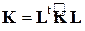 .
.
Дата добавления: 2016-01-29; просмотров: 777;
