Объединение конечных элементов

Пусть в расчетной модели сооружения имеется m КЭ и n узлов, а вектора ее перемещений и узловых нагрузок определены так:

,

.

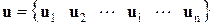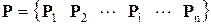После построения матриц жесткостей всех конечных элементов 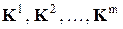и определения векторов узловых нагрузок 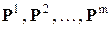в общей системе координат следует сформировать матрицу жесткости и вектор нагрузки всего сооружения. Это можно проделать так.

Вначале матрицы жесткости всех КЭов собираются в единую диаго-нальную матрицу 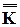, а вектора узловых нагрузок − в единый вектор :

, .

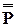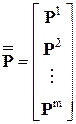Они еще не учитывают связи между соседними конечными элементами в узлах их примыкания.

Для объединения КЭов в единую систему используется энергетический принцип: энергия конечно-элементной модели системы равняется сумме энергий всех ее КЭ. В этом случае матрица жесткости объединенной системы будет определяться по формуле

,

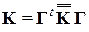где Г – объединяющая матрица. Элементы этой матрицы состоят только из нулей и единиц, а отдельные ее блоки соответствуют узлам КЭ и строятся по принципу: если КЭ содержит данный узел, то записывается единичная матрица, если нет – нулевая матрица. А соответствующие узловые нагрузки будут объединяться по формуле

.

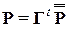Однако получение матрицы жесткости K и вектора нагрузки P таким способом требует больших вычислительных затрат. Задача упрощается, если составить так называемую матрицу индексов, определяющую соответствие номеров узловых перемещений КЭов узловым перемещениям всей модели. Тогда матрицу жесткости K можно получать рассылкой в ее блоки отдельных блоков матриц жесткостей КЭов по информации, заключенной в матрице индексов. При этом рассылка идет с суммированием рассылаемого блока матрицы жесткости КЭ с имеющимся блоком в матрице K. Такой метод называется методом сложения жесткостей.

Вектор узловой нагрузки P формируется аналогично.

В результате этих действий формируется разрешающее уравнение МКЭ, по виду совпадающее с уравнением МКЭ для отдельного КЭ:

Ku=P.

Но уже здесь K и P − матрица жесткости и вектор нагрузки всей системы. Матрицу K часто называют глобальной матрицей жесткости.