Геометрическое уравнение

Внешняя нагрузка приводит к деформации элементов сооружения, но при этом они не должны отрываться друг от друга. Это требование можно записать в виде уравнений совместности деформаций, отражающих геометрическую сторону задачи. Систему таких уравнений будем называть геометрическим уравнением.

Порядок составления геометрического уравнения изучим на примере рассмотренной в предыдущей лекции фермы (рис. 13.1 а).

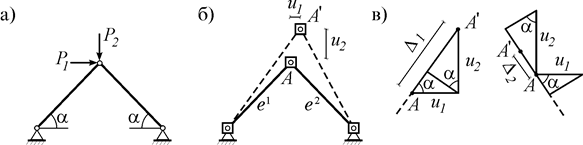
Рис. 13.1

Пусть под действием нагрузки элементы фермы получают только продольные деформации (рис. 13.1 б). Деформацию (удлинение) первого элемента e¹ можно определить по левой схеме на рис. 13.1 в:

.

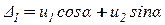Деформация второго элемента e² определяется по правой схеме рис. 1.1 в:

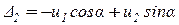
(из-за сжатия e² от перемещения 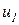первое слагаемое взято со знаком «–»).

Перепишем эти уравнения в виде

,

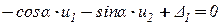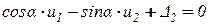
и представим в матричной форме

.

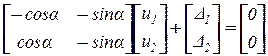Это уравнение можно записать в виде

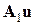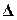+ =0, (1)

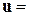
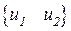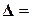
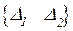где и – вектора перемещений и деформаций, 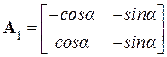– связующая матрица. Так как 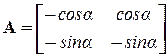– известная нам из предыдущей лекции матрица равновесия, то 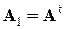(символ t означает операцию транспонирования). Значит, при получении уравнения (1) можно обойтись без громоздких геометрических построений и воспользоваться известной матрицей .

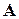Тогда уравнение (1) принимает вид

,

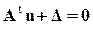которое и является искомым геометрическим уравнением.

Возможность использования одной и той же матрицы 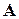в двух уравнениях – в уравнении статики и в геометрическом уравнении – называется принципом двойственности.