Представим эти уравнения в матричной форме

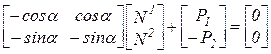
и обозначим входящие сюда матрицы и вектора:

, , , .

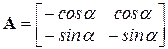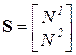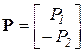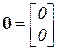В результате получим матричное уравнение

,

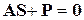которое называется уравнением равновесия, а входящие в него величины имеют следующие названия: A– матрица равновесия, S – вектор усилий, P – вектор нагрузки, 0 – нуль-вектор.

По матрице A можно установить некоторые особенности расчетной модели. Возможны три случая.

1. n = m (A – квадратная матрица размерности nxn). Если определитель матрицы A не равняется нулю (detA¹0), расчетная модель сооружения статически определима и геометрически неизменяема. В этом случае усилия определяются непосредственно из этого уравнения:

.

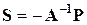Рассмотренная нами ферма является именно такой (n=m=2).

2. n< m. В этом случае система статически неопределима, а число m–n определяет степень ее статической неопределимости. Если ранг матрицы A равняется n, то такая система геометрически неизменяема.

3. n> m. Такая система геометрически изменяема.

В о п р о с ы

1. Какова сущность континуального подхода?

2. Что такое дискретный подход в механике?

3. Какова общая схема реализации различных методов расчета при дискретном подходе?

4. Как определяется дискретная модель стержневой системы?

5. Какой способ переноса нагрузки предпочтительнее и чем это обосновано?

6. Что такое уравнение равновесия и как оно получается?

7. Какие особенности расчетной модели можно установить по полученной матрице равновесия?

Л е к ц и я 13