Сущность метода перемещений
Данный вопрос изучим на следующем примере (рис. 10.4 а). Эта рама четырежды статически неопределима. При ее расчете методом сил нужно исключать четыре лишние связи и выбирать основную систему, например, такую как на рис. 10.4 б.
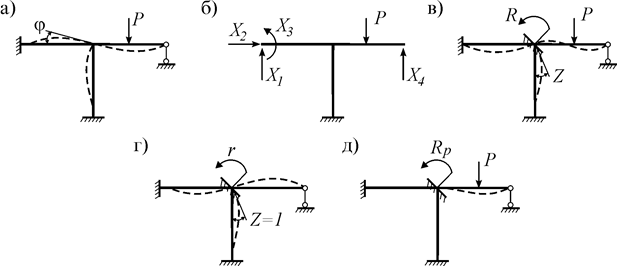
Рис. 10.4
При использовании же метода перемещений раму следует превратить в кинематически определимую. Для этого в ЗС достаточно ввести 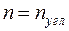 +
+ 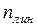 =1+0=1 кинематическую связь. Если неизвестное угловое перемещение узла обозначить через Z, получим ОС показанную на рис. 10.4 в.
=1+0=1 кинематическую связь. Если неизвестное угловое перемещение узла обозначить через Z, получим ОС показанную на рис. 10.4 в.
Потребуем, чтобы усилия и деформации ОС были такими же как у ЗС. Для этого перемещение Z должно быть равно углу поворота узла рамы j (рис. 10.4 а), а реактивный момент во введенной заделке основной системы (рис. 10.4 в) должен равняться нулю:
R =0.
Эту реакцию определим, рассматривая единичное и грузовое состояния основной системы.
В единичном состоянии введенной связи зададим единичное перемещение Z=1 и определим возникающую в ней реакцию r (рис. 10.4 г). Такая реакция от единичного перемещения называется жесткостью.
В грузовом состоянии приложим только внешнюю нагрузку и во введенной связи основной системы определим реакцию RP (рис. 10.4 д).
С учетом упругости системы и принципа суперпозиции наше уравнение приводится к виду
r · Z+ RP =0 .
Оно называется каноническим уравнением метода перемещений. Если известны реакции r и RP, то из него можно найти величину узлового перемещения:
Z= – RP /r.
Если степень кинематической неопределимости стержневой системы равна n, ее ОС получается введением n дополнительных связей с неизвестными Z1, Z2, …, Zn. Чтобы ОС была эквивалентна ЗС, реакции во введенных связях должны равняться нулю. С учетом этого можно записать n уравнений. После рассмотрения n единичных состояний, одного грузового состояния и дальнейшего определения реакций (реактивных усилий) во всех состояниях, эти уравнения приводятся к следующему виду:
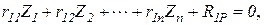
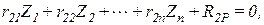 . . . . . . . . . . .
. . . . . . . . . . .
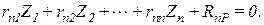
Все вместе они называются системой канонических уравнений метода перемещений. Здесь 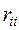 – главные коэффициенты,
– главные коэффициенты, 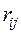 – боковые коэффициенты. Свободные члены
– боковые коэффициенты. Свободные члены 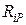 являются грузовыми коэффициентами.
являются грузовыми коэффициентами.
После введения матриц и векторов
r= 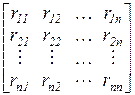 , Z =
, Z = 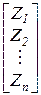 ,RP =
,RP = 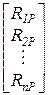 ,0 =
,0 = 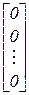
система канонических уравнений записывается в матричной форме: r · Z + RP = 0,
где r – матрица жесткости, Z – вектор неизвестных, RP – вектор нагрузки, 0 – нуль-вектор. Отсюда определяется вектор неизвестных:
Z = – r–1 RP,
где r–1 – обратная матрица жесткости.
В о п р о с ы
1. Какие величины являются неизвестными метода перемещений?
2. Что такое степень кинематической неопределимости?
3. Какие гипотезы принимаются при расчете рам методом перемещений?
4. Как определяется основная система метода перемещений?
5. Что называется жесткостью?
6. В чем заключается сущность метода перемещений?
7. Как записывается система канонических уравнений метода перемещений?
Л е к ц и я 11
Дата добавления: 2016-01-29; просмотров: 1126;
