Имитационное моделирование рисков на базе метода Монте-Карло.

Анализ рисков с использованием метода моделирования Монте-Карло (2, 3) представляет собой сочетание методов анализа чувствительности и анализа сцена­риев. Это достаточно сложная методика, имеющая под собой, как правило, компьютерную реализацию. Результатом такого анализа выступает распределение веро­ятностей возможных результатов проекта. Имитационное моделирование по мето­ду Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения пара­метров проекта, а также связь между изменениями параметров (корреляцию) по­лучить распределение доходности проекта.

При формировании сценариев с использованием методов имитационного моде­лирования применяется следующая последовательность действий:

1. определяются интервалы возможного изменения исходных переменных, внутри которых эти переменные являются случайными величинами;

2. определяются виды распределения вероятностей внутри заданных интервалов;

3. устанавливаются коэффициенты корреляции между зависимыми переменными;

4. многократно (не менее 200 раз) рассчитываются результирующие показатели;

5. полученные результирующие показатели рассматриваются как случайные вели­чины, которым соответствуют такие характеристики как: математическое ожи­дание, дисперсия, функция распределения и плотность вероятностей;

6. определяется вероятность попадания результирующих показателей в тот или иной интервал, вероятность превышения минимально допустимого значения и др.

Анализ значений результирующих показателей при сформированных сценари­ях позволяет оценить возможный интервал их изменения при различных условиях реализации проекта. Вероятностные характеристики используются для:

1. принятия инвестиционных решений;

2. ранжирования проектов;

3. обоснования рациональных размеров и форм резервирования и страхования.

На рис. 22.2.8. представлена схема работы с имитационной моделью (2,3).

Применение метода имитации Монте-Карло требует использования специаль­ных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master) , в то время, как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.

Результатом такого комплексного анализа выступает распределение вероятно­стей возможных результатов проекта (например, вероятность получения чистой дисконтированного дохода ЧДД).

Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая оказывает влияние на формирование потока наличности. Как правило, предполагается, что функция распределения яв­ляются нормальной, и, следовательно, для того, чтобы задать ее необходимо опре­делить только два момента (математическое ожидание и дисперсию).

Как только функция распределения определена, можно применять процедуру Монте-Карло.

Алгоритм метода имитации Монте-Карло

Шаг 1.Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения значение пере­менной, которая является одним из параметров определения потока наличности.

Шаг 2. Выбранное значение случайной величины наряду со значениями пере­менных, которые являются экзогенными переменными используется при подсчете чистой приведенной стоимости проекта.

Шаги 1 и 2 повторяются большое количество раз, например 1000, и получен­ные 1000 значений чистой приведенной стоимости проекта используются для по­строения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.

Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе методом сценариев.

Теперь необходимо определить минимальное и максимальное значения крити­ческой переменной, а для переменной с пошаговым распределением помимо этих двух еще и остальные значения, принимаемые ею. Границы варьирования пере­менной определяются, просто исходя из всего спектра возможных значений.

По прошлым наблюдениям за переменной можно установить частоту, с кото­рой та принимает соответствующие значения. В этом случае вероятностное распре­деление есть то же самое частотное распределение, показывающее частоту встре­чаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из определенного интерва­ла. В соответствии с заданным распределением модель оценки рисков будет выби­рать произвольные значения переменной. До рассмотрения рисков мы подразуме­вали, что переменная принимает одно определенное нами значение с вероятностью 1. И через единственную итерацию расчетов мы получали однозначно определен­ный результат. В рамках модели вероятностного анализа рисков проводится боль­шое число итераций, позволяющих установить, как ведет себя результативный по­казатель (в каких пределах колеблется, как распределен) при подстановке в мо­дель различных значений переменной в соответствии с заданным распределением.

Задача аналитика, занимающегося анализом рисков, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид веро­ятностного распределения. При этом основные вероятностные распределения, ис­пользуемые в анализе рисков, могут быть следующими: нормальное, постоянное, треугольное, пошаговое. Эксперт присваивает переменной вероятностное распреде­ление, исходя из своих количественных ожиданий и делает выбор из двух катего­рий распределений: симметричных (например, нормальное, постоянное, треуголь­ное) и несимметричных (например, пошаговое распределение).

Существование коррелированных переменных в проектном анализе вызывает порой проблему, не рассмотреть которую означало бы заранее обречь себя на не­верные результаты. Ведь без учета коррелированности, скажем, двух перемен­ных — компьютер, посчитав их полностью независимыми, генерирует нереали­стичные проектные сценарии. Допустим цена и количество проданного продукта есть две отрицательно коррелированные переменные. Если не будет уточнена связь между переменными (коэффициент корреляции), го возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной про­дукции будут вместе либо высоки, либо низки, что естественно негативно отразит­ся на результате.

Проведение расчетных итераций является полностью компьютеризированная часть анализа рисков проекта. 200-500 итераций обычно достаточно для хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соот­ветствии с вероятностными распределениями и условиями корреляции. Затем рас­считываются и сохраняются результативные показатели (например. ЧДД). И так далее, от итерации к итерации.

Завершающая стадия анализа проектных рисков -- интерпретация результатов, собранных в процессе итерационных расчетов. Результаты анализа рисков можно представить в виде профиля рисков. На нем графически показывается вероят­ность каждого возможного случая (имеются в виду вероятности возможных значе­ний результативного показателя).

Часто при сравнении вариантов капиталовложений удобнее пользоваться кри­вой, построенной на основе суммы вероятностей (кумулятивный профиль рисков). Такая кривая показывает вероятности того, что результативный показатель проек­та будет больше или меньше определенного значения. Проектный риск, таким об­разом, описывается положением и наклоном кумулятивного профиля рисков.

Кумулятивный (интегральный, накопленный) профиль рисков, показывает ку­мулятивное вероятностное распределение чистой текущей стоимости (ЧДД) с точки прения банкира, предпринимателя и экономиста на определенный проект. Вероят­ность того, что ЧДД 0 с точки зрения экономиста — около 0.4, в то время как для предпринимателя эта вероятность менее 0,2. С точки зрения банкира проект кажет­ся совсем безопасным, так как вероятность того, что ЧДД 0, около 95%.

Будем исходить из того, что проект подлежит рассмотрению и считается вы­годным, в случае, если ЧДД 0. При сравнении нескольких одноцелевых проектов выбирается тот, у которого ЧДД больше при соблюдении сказанного в предыду­щем предложении.

Пример.

Рассмотрим 5 иллюстративных случаев принятия решений (учебные материалы Институ­та экономического развития Всемирного банка). Случаи 1-3 имеют дело с решением инвести­ровать в отдельно взятый проект, тогда как два последних случая (4, 5) относятся к реше­нию-выбору из альтернативных проектов. В каждом случае рассматривается как кумулятив­ный, так и некумулятивный профили рисков для сравнительных целей. Кумулятивный профиль рисков более полезен в случае выбора наилучшего проекта из представленных аль­тернатив, в то время как некумулятивный профиль рисков лучше индуцирует вид распреде­ления и показателен для понимания концепций, связанных с определением математического ожидания. Анализ базируется на показателе чистой текущей стоимости.

Случай 1: Минимальное возможное значение ЧДД выше, чем нулевое (см. Рис. а, кри­вая 1)

Вероятность отрицательного ЧДД равна 0, так как нижний конец кумулятивного профи­ля рисков лежит справа от нулевого значения ЧДД. Так как данный проект имеет положи­тельное значение ЧДД во всех случаях, ясно, что проект принимается.

Случай 2: Максимальное возможное значение ЧДД ниже нулевого (см. Рис. а. кривая 2).

Вероятность положительного ЧДД равна 0 (см. следующий рисунок)., так как верхний конец кумулятивного профиля рисков лежит слева от нулевого значения ЧДД. Так как дан­ный проект имеет отрицательное значение ЧДД во всех случаях, ясно, что проект не прини­мается.

Случай 3: Максимальное значение ЧДД больше, а минимальное меньше нулевого (см. Рис а, кривая 3).

Вероятность нулевого ЧДД больше, чем 0, но меньше, чем 1, так как вертикаль нулевого ЧДД пересекает кумулятивный профиль рисков. Так как ЧДД может быть как отрицатель­ным, так и положительным, решение будет зависеть от предрасположенности к рискам инве­стора. По-видимому если математическое ожидание ЧДД меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику) проект должен отклоняться от дальнейшего рассмотрения.

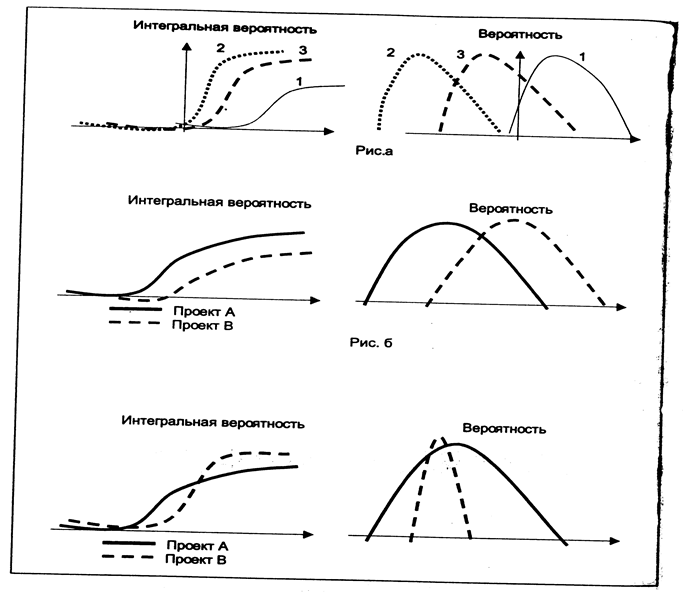
Случай 4: Непересекающиеся кумулятивные профили рисков альтернативных взаимоисключающих) проектов (см. Рис. б).

При фиксированной вероятности отдача проекта В всегда выше, нежели у проекта А. Профиль рисков также говорит о том, что при фиксированной ЧДД вероятность, с которой та будет достигнута, начиная с некоторого уровня будет выше для проекта В, чем для проекта А.

Если кумулятивные профили рисков двух альтернативных проектов не пересекаются ни в одной точке, тогда следует выбирать тот проект, чей профиль рисков расположен правее.

Сличай 5: Пересекающиеся кумулятивные профили рисков альтернативных проектов (см. Рис. в).

Склонные к риску инвесторы предпочтут возможность получения высокой прибыли и, таким образом, выберут проект А. Несклонные к риску инвесторы предпочтут возможность нести низкие потери и, вероятно, выберут проект В.

Несмотря на свои достоинства, метод Монте-Карло не распространен и не ис­пользуется слишком широко в бизнесе. Одна из главных причин этого — неопределенность функций распределения переменных, которые используются при расчетах.

Другая проблема, которая возникает как при использовании метода сценариев, так и при использовании метода Монте-Карло, состоит в том, что применение обоих методов не дает однозначного ответа на вопрос о том, следует ли все же реализовывать данный проект или следует отвергнуть его поэтому, как правило, используется целый комплекс методов анализа рисков проекта для окончательной оценки.

Общая результативность анализа проектных рисков (3) может быть оценена следующим образом:

Преимущества методов.

1. Совершенствует уровень принятия решений по малоприбыльным проектам. Проект с малым значением ЧДД может быть принят, в случае если анализ рисков установит, что шансы получить удовлетворительный доход превосходят ве­роятность неприемлемых убытков.

2. Помогает идентифицировать производственные возможности. Анализ рисков помогает сэкономить деньги, потраченные на получение инфор­мации, издержки на получение которой превосходят издержки неопределенности.

3. Освещает сектора проекта, требующие дальнейшего исследования и управляет сбором информации.

4. Выявляет слабые места проекта и дает возможность внести поправки.

5. Предполагает неопределенность и возможные отклонения факторов от базовых уровней. В связи с тем, что присвоение распределений и границ варьирования переменных несет оттенок субъективизма, необходимо критически подходить даже к результатам анализа рисков.

Сложности применения методов.

1. Проблема коррелированных переменных, которые, если неправильно специфицированы, могут привести к обманчивым заключениям.

2. Анализ рисков предполагает доброкачественность моделей проектного оценивания. Если модель неправильна, то результаты анализа рисков также будут вводить в заблуждение.