Оптимизация размера заказа.
Наиболее распространенным инструментом в управлении запасами, направленным на минимизацию суммарных затрат, традиционно признается модель оптимального размера заказа (EOQ). Причиной популярности этой модели является как простота математического аппарата, так и хорошие результаты ее практического использования.
Проблема управления запасами в данной модели сведена к определению объема заказа (Q) и частоты выполнения заказов (Т) за планируемый промежуток времени, что в свою очередь рассчитывается посредством балансирования между затратами, связанными с выполнением одного заказа (О), и затратами на хранение единицы запасов (С). Размер заказа следует увеличивать до тех пор, пока снижение затрат на заказ перевешивает увеличение затрат на хранение.
В наиболее простом варианте модели величина заказа Q и период между поставками Т принимаются постоянными величинами. Введенное в модель дополнительное ограничение по единовременной поставке новой партии в момент завершения запасов предыдущей, позволяет утверждать, что средний объем хранящихся
сто встречающиеся виды запасов на складе материалов ранен Q/2. Соответственно, издержки хранения запасов за период между двумя поставками равны произведению затрат хранения единицы материала на средний объем запасов.
Z1 = С х Q/2
Для расчета затрат по выполнению заказа к условию неизменной величины заказа прибавляется предположение о постоянной стоимости заказов, поэтому затраты по заказу определяются как произведение затрат на один заказ О и количество заказов за отчетный период (S/Q).
Z2 = S x O/Q,
где S — потребность в материалах или готовой продукции за отчетный период; Q — объем заказа; О — затраты, связанные с выполнением одного заказа.
Оптимальный размер заказа получается при минимальных суммарных издержках по управлению запасами
Z = Zl + Z2 -> MIN
Приравнивая первую производную от функции суммарных затрат к нулю, находим непосредственное значение оптимального размера заказа.
dZ/dQ = С/2 - (S x O)/Q2 = О
Таким образом, оптимальный размер заказа определяется:
Q = /(2 x S x О) / С
S — потребность в ресурсе = 900 ед. О — затраты на один заказ = 50 тыс. руб. С — затраты на хранение единицы ресурса = 11,25 тыс. руб. Тогда оптимальный заказ составляет: О= 89 изделий
Если повторный заказ поступает в течение L=10 дней, а в году 250 рабочих дней, то повторный заказ делается, когда уровень запаса падает до:
Р = (LxS)/250 = (10x900)7250 = 36 изделий
Эта формула предполагает, что заказ в 89 единиц делается, когда уровень запаса падает до 36 изделий. Последнее изделие будет использовано после того, когда поступит следующий заказ.
Средний объем запаса составляет 89/2 = 44,5 изделий.
Наиболее критичным фактором для эффективного использования модели является возможность оценить затраты на заказ и расходы на хранение.
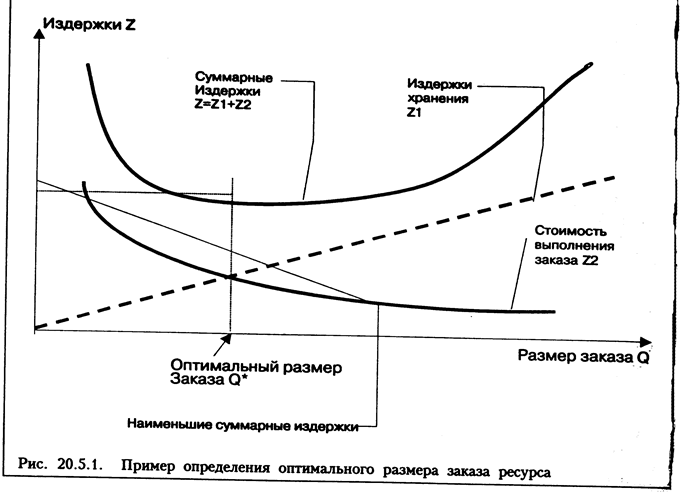
На рис. 20.5.1. проиллюстрировано определение оптимального размера запаса ресурса Q*. Он соответствует наименьшим суммарным издержкам.
В таблице 20.5.2. приведен алгоритм расчета параметров системы управления запасами.
Анализ примеров расчетов показывает, что:
1. резервный запас зависит от времени возможной задержки поставки и не зависит от времени поставки;
2. пороговый запас существенно зависит от суммарного времени поставки и возможно задержки поставки;
3. издержки на содержание резервного запаса завися! от возможной задержки поставки
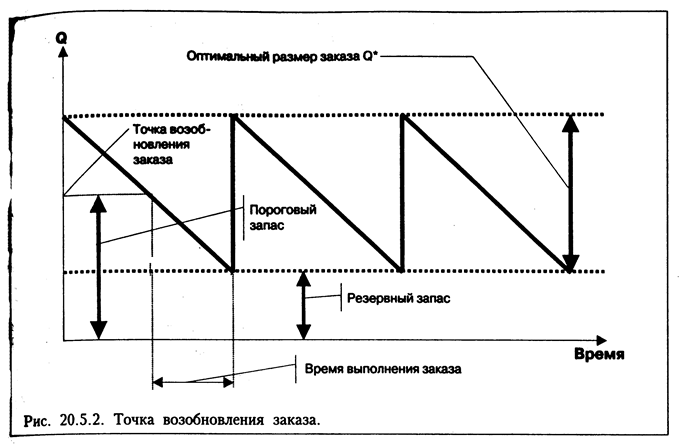
На рис. 20,5.2. представлен пример определения точки возобновления заказа
| Таблица 20.5.2. расчет параметров системы управления запасами | |||||
| Показатель | Порядок расчета | Пример расчета 1 | Пример расчета 2 | Пример расчета 3 | Пример расчета 4 |
| 1. Потребность, шт. | S | ||||
| 2. Затраты на хранение единицы ресурса, руб. | C | ||||
| 3. Затраты на поставку единицы ресурса, руб. | O | ||||
| 4. Оптимальный размер заказа | |||||
| 5. Время поставки | Тп | ||||
| 6. Возможная задержка поставки, дни | Тз | ||||
| 7. Ожидаемое дневное потребление, шт. день | P=S/250 | ||||
| 8. Срок расходования заказа, дни | Tp=Q/P | 100/4=25 | |||
| 9. Ожидаемое потребление за время поставки, шт. | Po=Tп×P | 24×4=96 | 23×4=92 | 24×4=96 | 23×4=92 |
| 10. Максимальное потребление за время поставки, шт. | Mп= (Tп+ Tз)×P | ||||
| 11. Резервный запас | Зр=Мп-Ро | ||||
| 12. Пороговый запас или точка заказа | Пз=Зр+Мп |
Дата добавления: 2016-01-29; просмотров: 1407;
