Сложение и вычитание двоичных чисел

Сложение чисел, а также вычитание чисел в обратном или дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Это правило распространяется и на знаковые разряды чисел. Различие же обратного и дополнительного кодов связано с тем, что потом делают с единицей переноса из старшего разряда, изображающего знак числа. При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда игнорируется. Это очевидно, если вспомнить, что дополнительный код из обратного получается как раз прибавлением единицы. Рассмотрим пример: сложить числа +18 и –7 (табл. 7.4).

Таблица сложения чисел в прямом и дополнительном кодах

Таблица 7. 4

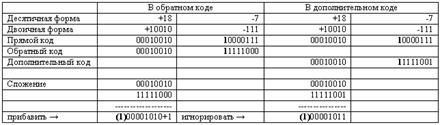
Итак, как в обратном, так и в дополнительном кодах результаты сложения совпали и равны 10112= 1110.

Умножение и деление двоичных чисел в ЭВМ производится в прямом коде, а их знаки используются лишь для определения знака результата. Также как и в математике, умножение и деление сводится к операциям сдвигов и сложений(с учётом знака числа).

Полученные коды мантиссы и порядка для каждого числа помещаются в ячейки памяти ЭВМ. Для каждой цифры, входящей в код, в ячейке памяти отводится своё отдельное место. Одна ячейка памяти состоит из 8 бит, т.е. 1 байта. В современных компьютерах 2 байта выделяются для одного машинного слова В последних моделях ПК обработка информации ведётся двойными словами, содержащими 4 байта. Числа с фиксированной запятой имеют формат одного слова, а числа с плавающей запятой - формат двойного слова..

Пример: Дано число с плавающей запятой величиной –0,625×10⁸. Нужно преобразовать его в машинный код и заполнить 32-разрядную ячейку памяти. Мантисса числа 0,625₁₀ = 0,101₂. Поскольку порядок чисел может быть как положительным, так и отрицательным, то машинный порядок смещается относительно естественного таким образом, чтобы весь диапазон машинных порядков изменялся от 0 до максимума, определяемого количеством разрядов, выделяемых для размещения чисел порядка. Обычно в 32-разрядной ячейке цифры порядка занимают 7 разрядов старшего байта, а восьмой разряд используется для фиксации знака числа. Семь двоичных разрядов позволяют разместить диапазон десятичных разрядов от –64 до +63. Если обозначить машинный порядок через R, а естественный через r, то связь между ними будет такая: R₁₀ = r₁₀+64₁₀. Для двоичной системы счисления R₂ = r₂ + 1000000₂. В нашем примере порядок r равен 8₁₀ = 1000₂, следовательно R₂ = 1001000. В двоичной системе исходное число выглядит так: –0,101х10¹⁰⁰⁰. Запись этого числа в 32-разрядной ячейке представлена в табл. 7.5:

Сводная таблица переводов целых чисел

Таблица 7. 5

Вопросы для ПОВТОРЕНИЯ И самоконтроля

1. Для чего нужно изучать системы счисления, которые используются в компьютере?
2. Что называется системой счисления?
3. На какие два типа можно разделить все системы счисления?
4. Какие системы счисления называются непозиционными? Почему? Приведите пример такой системы счисления и записи чисел в ней?
5. Какие системы счисления применяются в вычислительной технике: позиционные или непозиционные? Почему?
6. Какие системы счисления называются позиционными?
7. Как изображается число в позиционной системе счисления?
8. Что называется основанием системы счисления?
9. Что называется разрядом в изображении числа?
10. Как можно представить целое положительное число в позиционной системе счисления?
11. Приведите пример позиционной системы счисления.
12. Опишите правила записи чисел в десятичной системе счисления:
    i. а) какие символы образуют алфавит десятичной системы счисления?
    ii. б) что является основанием десятичной системы счисления?
    iii. в) как изменяется вес символа в записи числа в зависимости от занимаемой позиции?
13. Какие числа можно использовать в качестве основания системы счисления?
14. Какие системы счисления применяются в компьютере для представления информации?
15. Охарактеризуйте двоичную систему счисления: алфавит, основание системы счисления, запись числа.
16. Почему двоичная система счисления используется в информатике?
17. Дайте характеристику шестнадцатеричной системе счисления: алфавит, основание, запись чисел. Приведите примеры записи чисел.
18. Дайте характеристику восьмиричной системе счисления: алфавит, основание, запись чисел. Приведите примеры записи чисел.
19. По каким правилам выполняется сложение двух положительных целых чисел?
20. Каковы правила выполнения арифметических операций в двоичной системе счисления?
21. Для чего используется перевод чисел из одной системы счисления в другую?
22. Сформулируйте правила перевода чисел из системы счисления с основанием р в десятичную систему счисления и обратного перевода: из десятичной системы счисления в систему счисления с основанием р. Приведите примеры.
23. В каком случае для перевода чисел из одной системы счисления в другую может быть использована схема Горнера вычисления значения многочлена в точке? Каковы преимущества ее использования перед другими методами? Приведите пример.
24. Как выполнить перевод чисел из двоичной системы счисления в восьмеричную и обратный перевод? Из двоичной системы счисления в шестнадцатеричную и обратно? Приведите примеры. Почему эти правила так просты?
25. По каким правилам выполняется перевод из восьмеричной в шестнадцатеричную системы счисления и наоборот? Приведите примеры.
26. Напишите таблицы правил выполнения двоичного сложения, вычитания и умножения.
27. Какая форма представления информации называется непрерывной, а какая – дискретной?
28. Какая форма представления информации – непрерывная или дискретная – приемлема для компьютеров и почему?
29. Какова единица измерения информации?
30. Как задаются производные единицы измерения информации?
31. Как определяется алфавит?
32. Как кодируются символы в памяти компьютера?
33. Что собой представляет таблица ASCII кодов?
34. Как кодируются целые положительные числа в памяти компьютера?
35. Каковы особенности представления целых отрицательных чисел в памяти компьютера?

36. Как кодируются действительные числа?