Перевод чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода[8].

Правило 1

Для перевода чисел из любой системы счисления в десятичную, можно воспользоваться выражением (7.1). Сначала в десятичную систему счисления переводится основание той системы, из которой осуществляется перевод, а затем цифры исходного числа. Результаты подставляются в выражение (7.1). Полученная сумма дает искомый результат.

Пример

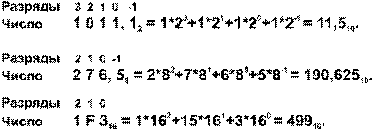
Схема Горнера

Эквивалентными являются алгоритмы для вычисления значения многочлена в некоторой точке х, заданные следующими формулами:

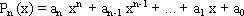
(7.5)

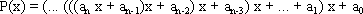
(7.6)

Запись (7.6) носит название вычислительной схемы Горнера.

Например:

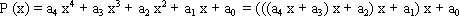
Алгоритм, задаваемый формулой (7.6) требует меньше арифметических операций и сводится к выполнению последовательной цепочки операций умножения и сложения в порядке их записи слева направо, поэтому при переводе чисел в десятичную систему счисления можно воспользоваться схемой Горнера.

Правило 2

Для перевода целых чисел из десятичной системы счисления в систему счисления с основанием р надо:

Последовательно делить заданное число и получаемые целые части на новое основание счисления р до тех пор, пока целая часть не станет меньше нового основания счисления.

Полученные остатки от деления, представленные цифрами из нового счисления, записать в виде числа, начиная с последней целой части.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную (рис. 7.2):

в двоичную в восьмиричную в шестнадцатиричную

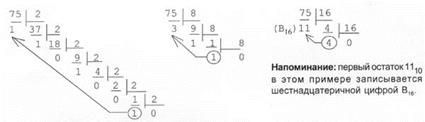
Рис. 7. 2. Перевод числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Правило 3

Для перевода правильной десятичной дpоби F в систему счисления с основанием р необходимо F умножить на р , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на р, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в р -ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной р -ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную (рис. 7.3):

Рис. 7. 3. Перевод дробного числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам 2 и 3.

Правило 4

Преобразования чисел из двоичной в восьмеричную и шестнадцатеричную системы и наоборот просты потому, что числа 8 и 16 являются целыми степенями числа 2.

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Лишние нули в старших разрядах отбрасываются.

Пример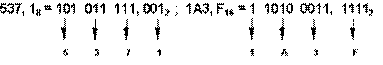

Правило 5

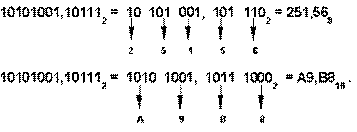
Обратный перевод производится так: каждая триада двоичных цифр заменяется восьмеричной цифрой, а каждая тетрада двоичных цифр заменяется шестнадцатеричной цифрой. Для правильного перевода число должно быть выровнено, т.е. число двоичных знаков должно быть кратно трем (для восьмеричной цифры) или четырем (шестнадцатеричнойцифры) Выравнивание производится простым дописыванием требуемого количества нулей перед старшим разрядом целой части числа.

Пример

Сводная таблица переводов целых чисел из одной системы счисления в другую

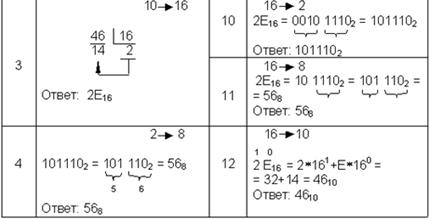
Рассмотрим десятичную, двоичную, восьмеричную и шестнадцатеричную системы счисления, которые применяются в компьютерах. Возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рис. 7.4:

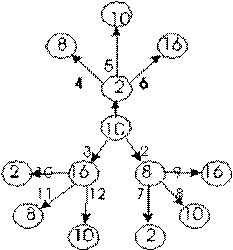
Рис. 7. 4. Сводная схема переводов целых чисел из одной системы счисления в другую

На этом рисунке использованы следующие обозначения: в кружках записаны основания систем счисления; стрелки указывают направление перевода; номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 7.3.

Сводная таблица переводов целых чисел

Таблица 7. 3

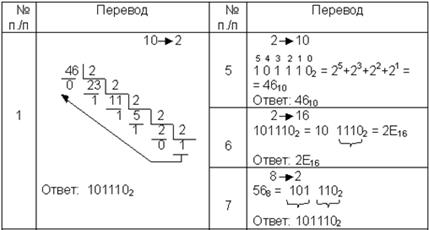
Продолжение табл. 7.3.

7.3. Арифметические операции,
выполняемые в позиционных системах счисления

В вычислительной технике наиболее часто выполняется операция сложения. Вычисления выполняются по следующим правилам:

- операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;

- в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;

- если сумма цифр одноименных разрядов слагаемых и переноса меньше основания системы счисления, то перенос в следующий разряд равен нулю, если равна или больше — то равен единице.

В качестве примера рассмотрим арифметические операции в десятичной и двоичной системе счисления.

Арифметические операции над числами в двоичной системе счисления

Рассмотрим правила выполнения арифметических операций над однозначными числами. Представим е

Сложение

Пример 1. Сложим числа 15 и 6.

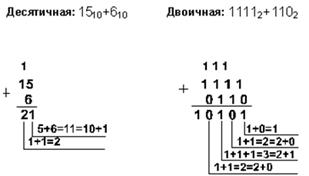
Проверка. Преобразуем полученные суммы к десятичному виду: 101012 =
2⁴ + 2² + 2⁰ = 16+4+1=21.

Пример 2. Сложим числа 141,5 и 59,75.

Проверка. Преобразуем полученные суммы к десятичному виду:

11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25

Вычитание

Пример 3. Вычтем единицу из чисел 10₂ и 100₂

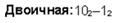
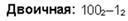
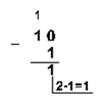
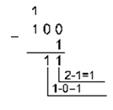
Пример 4.Вычтем число 59,75 из числа 201,25

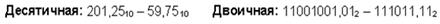
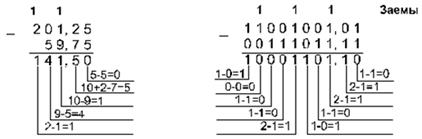
Проверка. Преобразуем полученные разности к десятичному виду:

10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^-1 = 141,5;

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример 5. Перемножим числа 5 и 6.

Проверка. Преобразуем полученные произведения к десятичному виду:

11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;

Пример 6. Перемножим числа 115 и 51.

Проверка. Преобразуем полученные произведения к десятичному виду:

1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;