ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. 1. Первая ламповая ЭВМ называлась:
1. Первая ламповая ЭВМ называлась:
1. Марк-1;
2. ЭНИАК;
3. Цузе 1.
2. Кто из перечисленных ученых не связан с историей создания вычислительных машин:
1. Джордж Буль;
2. Чарльз Беббидж;
3. Исаак Ньютон;
4. Леонардо да Винчи.
3. Первые ЭВМ были созданы в XX веке...
1. В 40-е годы;
2. В 60-е годы;
3. В 70-е годы;
4. В 80-е годы.
4. Основной элементной базой ЭВМ четвертого поколения являются:
полупроводники;
1. Электромеханические схемы;
2. Электровакуумные лампы;
3. СБИС.
ОТВЕТЫ НА ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Верные ответы: 2;
2. Верные ответы: 3;
3. Верные ответы: 1;
4. Верные ответы: 3;
ГЛАВА 7.СИСТЕМЫ СЧИСЛЕНИЯ. АРИФМЕТИКА В РАЗЛИЧНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
Системы счисления
Изучение систем счисления, которые используются в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ.
Система счисления — способ записи чисел с помощью заданного набора специальных символов (цифр) и сопоставления этим записям реальных значений.
Все системы счисления можно разделить на непозиционные и позиционные.
В непозиционных системах счисления, которые появились значительно раньше позиционных, смысл каждого символа не зависит от того места, на котором он стоит. Примером такой системы счисления является Римская, в которой для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV.
Недостатком непозиционных систем является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Правила выполнения вычислений с многозначными числами в позиционной системе счисления были разработаны средневековым математиком Мухамедом аль-Хорезми и в Европе были названы алгоритмами (от латинского написания имени аль-Хорезми – Algorithmi).
В вычислительной технике применяются позиционные системы счисления. Позиционных систем счисления существует множество, и отличаются они друг от друга алфавитом — множеством используемых цифр. Размер алфавита (число цифр в нем) называется основанием системы счисления. Последовательная запись символов алфавита (цифр) изображает число. Позиция символа в изображении числа называется разрядом. Разряду с номером 0 соответствует младший разряд целой части числа. Каждому символу соответствует определенное число, которое меньше основания системы счисления. В зависимости от позиции (разряда) числа значение символа умножается на степень основания, показатель которой равен номеру разряда.
Таким образом, целое положительное число А в позиционной системе счисления можно представить выражением:
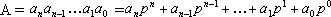
| (7.1) |
или 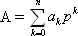 ,
,
где p — основание системы счисления, целое положительное число; a — cимвол (цифра); n — номер старшего разряда числа.
Обозначения цифр берутся из алфавита, который содержит p символов. Каждой цифре соответствует определенный количественный эквивалент. Обозначение ak следует понимать как цифру в k-м разряде. Всегда выполняется неравенство: ak<p.
Запись A(p) указывает, что число А представлено в системе счисления с основанием р:
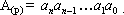
| (7.2) |
Примером системы счисления является всем нам хорошо известная десятичная система счисления. Любое число в ней записывается с помощью цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Важно, что значение каждой цифры зависит от того места, на котором она стоит в этой записи.
Например, 1575: цифра 5 в записи числа встречается дважды: цифра 5 в последнем разряде — число единиц, а цифра 5, находящаяся в записи числа левее, — число сотен. В десятичной системе счисления значение единицы каждого разряда в 10 раз больше единицы соседнего с ним правого разряда.
Само число 10 называется основанием системы счисления, а цифры, используемые в десятичной системе — базисными числами этой системы.
Но в качестве основания системы счисления можно выбрать любое целое число.
В компьютере для представления информации используются десятичная, двоичная, восьмиричнаяи шестнадцатеричная системы счисления. Количество цифр, которое требуется для изображения числа в позиционной системе счисления, равно основанию системы счисления р. Например, для записи чисел в двоичной системе счисления требуется две цифры, в десятичной — десять, а в шестнадцатеричной — шестнадцать.
Двоичная система счисления имеет набор цифр {0, 1}, р=2. В общем виде, используя формулу (7.1), двоичное число можно представить выражением:
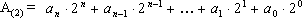
| (7.3) |
Например, число 101101(2) можно записать так:
1011012 = 1*25+0*24+1*23+1*22+0*21+1*20
Открытие двоичного способа представления чисел приписывают китайскому императору Фо Ги, жизнь которого относится к 4-му тысячелетию до новой эры. Известный немецкий математик Лейбниц (рис. 6.15) в 1697 г. разработал правила двоичной арифметики. Он подчеркивал, что "вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот, является для науки основным и порождает новые открытия, которые оказываются полезными впоследствии, даже в практике чисел, а особенно в геометрии: причиной чего служит то обстоятельство, что при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок".
Блестящие предсказания Лейбница сбылись только через 2,5 столетия, когда именно двоичная система счисления нашла применение в качестве универсального способа кодирования информации в компьютерах.
Шестнадцатеричная система счисления имеет набор цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}, p = 16. Для изображения чисел в шестнадцатеричной системе счисления требуются 16 цифр. Для обозначения первых десяти цифр используются цифры десятичной системы счисления, шесть остальных — первых шесть прописных букв латинского алфавита. По формуле (7.1) шестнадцатеричное число может быть представлено так:
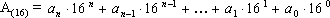
| (7.4) |
Пример. Число E7F8140 по формуле (7.4) запишется так:
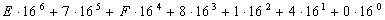
Восьмиричная система счисления имеет набор цифр {0, 1, 2, 3, 4, 5, 6, 7}, p = 8. Для изображения чисел в восьмиричной системе счисления требуются 8 цифр. Восьмиричная система используется реже, но ее тоже полезно знать.
Представление информации, хранящейся в памяти компьютера, в ее истинном двоичном виде весьма громоздко из-за большого количества цифр.
Каждый разряд двоичного числа имеет информационную емкость 1 бит. На основании одного двоичного разряда можно закодировать только два десятичных числа. На основании двух двоичных разрядов можно закодировать уже четыре десятичных числа. Тремя двоичными разрядами можно представить восемь десятичных чисел и т.д
Мы видим, что добавление каждого следующего разряда вдвое увеличивает количество двоичных комбинаций. Графически это может быть представлено так (рис. 7.1):
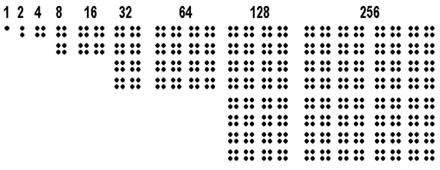
Рис. 7. 1. Принцип удвоения количества возможных комбинаций из нулей и единиц при увеличении разрядности
Поэтому при записи двоичной информации на бумаге или выводе ее на экран принято использовать восьмеричную или шестнадцатеричную системы счисления. В современных компьютерах чаще используется шестнадцатеричная система счисления.
Полезно помнить некоторые степени двойки, восьмерки и шестнадцати (табл. 7.1).
Степени двойки, восьмерки и шестнадцати
Таблица 7. 1
| k | 2k | 8k | 16k |
Запись в этих системах счисления первых двух десятков целых чисел приведена в табл. 7.2:
Соответствие чисел в различных системах счисления
Таблица 7. 2
| 10-я | 2-я | 8-я | 16-я | 10-я | 2-я | 8-я | 16-я |
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F | |||||||
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
- для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел (см. табл. 7.2).
Дата добавления: 2015-11-26; просмотров: 4971;
