ГЛАВА 8. АЛГЕБРА ЛОГИКИ
8.1. Возникновение логики
как самостоятельной науки
Понятие логики как науки появилось ещё в XIX в., т.е. задолго до появления науки информатики и компьютеров. Элементы математической логики можно найти уже в работах древнегреческих философов.
Логику, основанную Аристотелем (384–322 до н. э. - крупнейший древнегреческий мыслитель), принято называть формальной. Это название закрепилось за ней потому, что она возникла и развилась как наука о формах мышления.
В XVII в. Г. В. Лейбниц высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам. Однако как самостоятельный раздел математики логика начала формироваться только с середины XIX в..
Для того чтобы рассуждать, человеку необходим какой-либо язык. Не удивительно, что математическая логика начиналась с анализа того, как говорят и пишут люди на естественных языках. Этот анализ привёл к тому, что выяснилось существование формулировок, которые невозможно разделить на истинные и ложные, но, тем не менее, выглядят осмысленным образом. Это приводило к возникновению парадоксов, в том числе в одной из фундаментальных наук математики. Тогда было решено создать искусственные формальные языки, лишённого «вольностей» языка естественного.

Рис. 8. 1. Джордж Буль – английский математик-самоучка
Джордж Буль (1815-1864г) по праву считается отцом математической логики (рис. 8.1). Его именем назван раздел математической логики – булева алгебра.
Буль изобрел своеобразную алгебру - систему обозначений и правил, применимую ко всевозможным объектам, от чисел до предложений. Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами.
Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным.
А еще несколько десятилетий спустя, уже в ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Рис. 8. 2. Клод Шеннон – американский математик
В 1936 году выпускник Мичиганского университета Клод Шеннон (1916-2001г), которому был тогда 21 год, сумел ликвидировать разрыв между алгебраической теорией логики и ее практическим приложением (рис. 8.2).
Шеннон, имея два диплома бакалавра - по электротехнике и по математике, выполнял обязанности оператора на неуклюжем механическом вычислительном устройстве под названием "дифференциальный анализатор"
Постепенно у Шеннона стали вырисовываться контуры устройства компьютера. Если построить электрические цепи в соответствии с принципами булевой алгебры, то они могли бы выражать логические отношения, определять истинность утверждений, а также выполнять сложные вычисления. Свои идеи относительно связи между двоичным исчислением, булевой алгеброй и электрическими схемами Шеннон развил в докторской диссертации, опубликованной в 1938 году.
Применение в вычислительной технике и информатике алгебры логики
После изготовления первого компьютера стало ясно, что при его производстве возможно использование только цифровых технологий – ограничение сигналов связи единицей и нулём для большей надёжности и простоты архитектуры ПК. Благодаря своей бинарной природе, математическая логика получила широкое распространение в ВТ и информатике. Были созданы электронные эквиваленты логических функций, что позволило применять методы упрощения булевых выражений к упрощению электрической схемы. Кроме того, благодаря возможности нахождения исходной функции по таблице позволило сократить время поиска необходимой логической схемы.
В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1 - истина” и “0 - ложь”.
Из этого следует два вывода:
- Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.
- На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов компьютера.
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.
Логическими элементами компьютеров являются электронные схемыИ, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210 = 8192 триггеров. Современные микросхемы памяти содержат миллиарды триггеров.
8.2. Понятие “алгебры логики” как науки об общих операциях над логическими высказываниями[10]
Алгебра логики — это раздел математики, изучающийвысказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Так, например, предложение "Меню в программе – это список возможных вариантов" следует считать высказыванием, так как оно истинное. Предложение "Город Джакарта – столица Микронезии" тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "Какого цвета этот дом?" и "Эта тема скучна". Первое предложение вопросительное, а не повествовательное. Второе использует слишком неопределённое понятие "тема скучна".
Предложения типа "Рикки Мартин – самый популярный певец" не являются высказываниями, так как для выяснения его истинности или ложности нужны дополнительные сведения: о каком конкретно регионе, или о какой группе людей идет речь. Такие предложения называются высказывательными формами.
Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Часто трудно установить истинность высказывания. Так, например, высказывание "Численность жителей города Красноярска составляет 961 тыс. чел" может быть одновременно истинным и ложным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными. Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Зимой люди катаются на коньках", а через В — высказывание "Зимой люди катаются на лыжах".
Тогда составное высказывание "Зимой люди катаются на коньках и на лыжах" можно кратко записать как А и В. Здесь "и" — логическая связка, А, В — логические переменные, которые мoгут принимать только два значения — "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение. Базовыми являются пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция. Каждую логическую операцию можно иллюстрировать таблицей истинности.
Таблица истинности это табличное представление логической операции, в котором перечислены все возможные сочетания значений истинности входных операндов вместе со значением истинности выходного результата операции для каждого из этих сочетаний.
НЕ.Операция, выражаемая словом "НЕ", называется отрицанием и обозначается чертой над высказыванием (или знаком 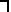 ). Высказывание
). Высказывание 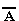 истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" (
истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" ( 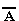 ). Таблица истинности логической операции "не" приведена в табл. 8.1.
). Таблица истинности логической операции "не" приведена в табл. 8.1.
Таблица истинности логического отрицания "НЕ"
Таблица 8. 1
| x | 
|
И.Операция, выражаемая связкой "И", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками 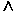 или *). Высказывание А.и В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше3" — ложны. Таблица истинности логической операции "и" приведена в табл. 8.2.
или *). Высказывание А.и В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше3" — ложны. Таблица истинности логической операции "и" приведена в табл. 8.2.
Таблица истинности логического умножения (конъюнкции) "И"
Таблица 8. 2
| Х | У | Х^У |
ИЛИ.Операция, выражаемая связкой "ИЛИ" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", — истинны. Таблица истинности логической операции "или" приведена в табл. 8.3.
Таблица истинности логического сложения (дизъюнкции) "ИЛИ"
Таблица 8. 3
| Х | У | ХVУ |
ЕСЛИ-ТО. Операция, выражаемая связками "если ..., то", "из ... следует", "... влечет ...", называется импликацией (лат. implico — тесно связаны) и обозначается знаком 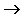 или
или 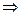 . Высказывание
. Высказывание 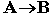 ложно тогда и только тогда, когда А истинно, а В ложно. Таблица истинности логической операции "импликация" приведена в табл. 8.4.
ложно тогда и только тогда, когда А истинно, а В ложно. Таблица истинности логической операции "импликация" приведена в табл. 8.4.
Таблица истинности импликации "ЕСЛИ-ТО"
Таблица 8. 4
| х | у | х—›у |
В обычной речи связка "если ..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность.
РАВНОСИЛЬНО. Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией или двойной импликацией и обозначается знаком 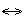 или ~. или ÛВысказывание
или ~. или ÛВысказывание 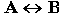 истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 3 - истино, а высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 5" - ложно. Таблица истинности логической операции "эквиваленции" приведена в табл. 8.5.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 3 - истино, а высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 5" - ложно. Таблица истинности логической операции "эквиваленции" приведена в табл. 8.5.
Таблица истинности эквиваленция, связка "Тогда и только тогда" Таблица 8. 5
| х | у | х‹—›у |
Импликацию можно выразить через дизъюнкцию и отрицание:
А 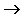 В =
В = 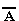 v В.
v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А 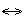 В = (
В = ( 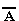 v В) . (
v В) . ( 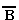 v А).
v А).
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
8.3. логическая формул.
законы алгебрЫ логики
Логические формулы
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.
Если А и В — формулы, то 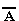 , А . В , А v В , А
, А . В , А v В , А  B , А
B , А  В — формулы.
В — формулы.
Дата добавления: 2015-11-26; просмотров: 2706;
