Системы логических элементов

Системой логических элементов называется функционально полный набор логических элементов, объединенных общими электрическими, конструктивными и технологическими параметрами и использующих одинаковый тип межэлементных связей [69].

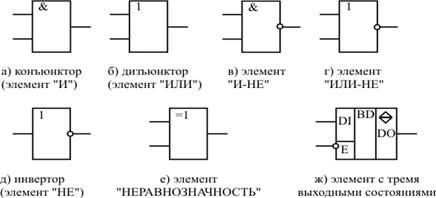
Рис. 8. 3. Условно-графические обозначения логических элементов

Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также элементы для усиления, восстановления и формирования сигналов стандартной формы.

Условно-графические обозначения (УГО) некоторых логических элементов представлены на рис. 8.3.

УГО элемента представляет собой прямоугольник, к которому слева подходят входные сигналы, а справа выходят выходные. Внутри прямоугольника ставится условное обозначение выполняемой элементом логической функции. Если значение выходного сигнала принимает инверсное значение по отношению к обозначенной внутри элемента функции, то данный выход обозначается на УГО элемента кружком (рис. 8.3.в …8.3.д). Аналогично, если активным уровнем входного сигнала является логический "0", то данный вход обозначается кружком (вход E элемента 8.3.ж).

Таблицы истинности для УГО инвертера (элемента "НЕ), конъюнктора (элемента "И"), дизъюнктора (элемента "ИЛИ") приведены в параграфе 8.2 в таблицах 8.1, 8.2, 8.3 соответственно.

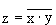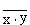Элемент "И—НЕ" состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: , где читается как "инверсия x и y". Для элемента "И-НЕ" (рис. 8.3.в) возможные состояния описываются таблицей 8.10.

Таблица истинности "И-НЕ"

Таблица 8. 10

Элемент "ИЛИ—НЕ" состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.

Таблица истинности "ИЛИ-НЕ"

Таблица 8. 11

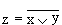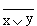Связь между выходом выходом z и входами x и y схемы записывают следующим образом: , где , читается как "инверсия x или y". Для элемента "ИЛИ-НЕ" (рис. 8.3.г) возможные состояния описываются таблицей 8.11.

Вопросы для ПОВТОРЕНИЯ И самоконтроля

1. Кто разработал формальную логику и почему она так называется?

2. Какуюидею высказал Г. В. Лейбниц о рассуждениях?

3. Кто является основателем математической логики?

4. Кто из наших современников сумел ликвидировать разрыв между алгебраической теорией логики и ее практическим приложением?

5. Почему математический аппарат алгебры логики удобен для описания того, как функционируют аппаратные средства компьютера?

6. Для чего служит электронная схема "вентиль"?

7. Что такое "триггер"?

8. Сформулируйте понятие алгебры логики.

9. Что такое "логическое высказывание"?

10. Что такое "высказывательная форма" логического высказывания?

11. Какие слова относятся к "логическим связкам (операциям)"?

12. Что такое "составное"и"элементарное"высказывание?

13. Охарактеризуйте понятие "таблица истинности".

14. "Логическое отрицание" – обозначение и таблица истинности.

15. "Логическое умножение " – обозначение и таблица истинности.

16. "Логическое сложение " – обозначение и таблица истинности.

17. "Импликация " – обозначение и таблица истинности.

18. "Эквиваленция " – обозначение и таблица истинности.

19. Через какие другие логические функции можно выразить импликацию и эквиваленцию?

20. Что понимается под логической формулой?

21. Что такое выполнимая логическая формула?

22. Что такое тождественно истиннаялогическая формула?

23. Что такое тождественно ложнаялогическая формула?

24. Что такое равносильнаялогическая формула?

25. Основные законы алгебры логики.

26. Какое количество наборов значений переменных необходимо написать в таблице истинности для N переменных?

27. Как решаются таблицы истинности?