Приведение масс и моментов инерции.
Операция приведения осуществляется для каждого звена, а затем приведенные моменты инерции cсуммируются. При этом используетсяусловие равенства кинетических энергий. Расчетные формулы зависят от вида движения звена (в плоских механизмах три варианта). Если звено совершает поступательное движение, то
= 
,
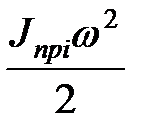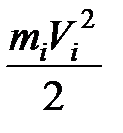где mi – масса звена, Vi – скорость звена. Откуда
Jпр i =m i (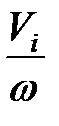 
)2=mi(S¢ i )2. (15.4)
Если звено совершает вращательное движение, то
= 
,
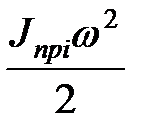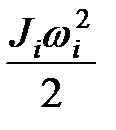где Ji – момент инерции звена относительно оси вращения,
wi – угловая скорость звена.
Тогда Jпр i =Ji (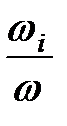 
)2. (15.5)
Если звено совершает сложно-плоское движение, то получим
= 
+ 
,
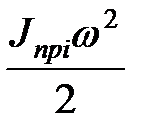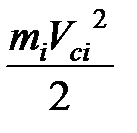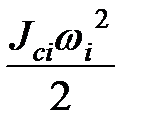где Vci – скорость центра масс звена, Jci– момент инерции звена относительно центра масс. Поэтому
Jпр i = mi (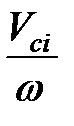 
)2 + Jci ( 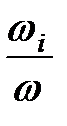)2.(15.6)
Общий приведенный момент инерции Jпр =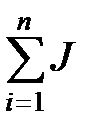 
ПР i.
Из анализа формул (15.4), (15.5), (15.6) следует, что JПР в общем случае является переменной величиной, зависящей от положения механизма.
Можно записать Jпр = Jc+Jv : (15.7)
здесь Jc – постоянная часть приведённого момента инерции (от звеньев, совершающих вращательное движение);
Jv – переменная часть приведённого момента инерции (от звеньев, совершающих возвратно-поступательное, качательное и сложно-плоское движение ).
Дата добавления: 2016-01-26; просмотров: 825;