Динамика движения материальной точки по окружности. Центростремительная и тангенциальная силы. Плечо и момент силы. Момент инерции. Уравнения вращательного движения точки
В данном случае материальной точкой можно считать тело, размеры которого малы по сравнению с радиусом окружности.
В подразделе (3.6) было показано, что ускорение тела, движущегося по окружности, складывается из двух составляющих (см. рис. 3.20): центростремительного ускорения — ац тангенциального ускорения ат, направленных по радиусу и касательной соответственно. Эти ускорения создаются проекциями равнодействующей силы на радиус окружности и касательную к ней, которые называются центростремительной силой (F ) и тангенциальной силой (FT) соответственно (рис. 4.5).
ft
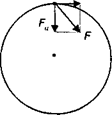
Рис. 4.5.Компоненты равнодействующей силы при неравномерном вращательном движении
Центростремительной силойназывается проекция равнодействующей силы на тот радиус окружности, на котором в данный момент находится тело.
Тангенциальной силойназывается проекция равнодействующей силы на касательную к окружности, проведенную в той точке, в которой в данный момент находится тело.
Роль этих сил различна. Тангенциальная сила обеспечивает изменение величины скорости, а центростремительная сила вызывает изменение направления движения. Поэтому для описания вращательного движения записывают второй закон Ньютона для центростремительной силы:
Fц=т·ац.
(4.11)
Здесь т — масса материальной точки, а величина центростремительного ускорения определяется по формуле (4.9).
В ряде случаев для описания движения по окружности удобнее использовать не центростремительную силу (Fц ), а момент силы, действующей на тело. Поясним смысл этой новой физической величины.
Пусть тело вращается вокруг оси (О) под действием силы, которая лежит в плоскости окружности.
Кратчайшее расстояние от оси вращения до линии действия силы (лежащей в плоскости вращения) называется плечом силы (h).
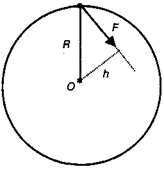
Рис. 4.6.Плечо силы (h)
На рис. 4.6 показаны действующая сила и ее плечо.
Моментом силы(М) относительно оси вращения называется произведение величины силы на ее плечо:
M = ±F·h. (4.12)
Момент силы берется со знаком «+», если сила стремится повернуть тело по часовой стрелке и со знаком «—» в противном случае.
Примечание. В некоторых случаях момент силы считают вектором, направленным по оси вращения. В данном учебнике такие случаи не рассматриваются.
Можно показать, что угловое ускорение (ε), с которым материальная точка движется по окружности, прямо пропорционально моменту (М) действующей на него силы:
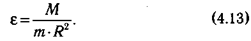
Величина, входящая в знаменатель формулы (4.13), называется моментом инерции.
Моментом инерции(J) материальной точки относительно оси вращения называется произведение ее массы (т) на квадрат расстояния (R) до оси вращения:
J = m·R2. (4.14)
Из определения следует, что измеряется момент инерции в кг·м2.
Подставив момент инерции (4.14) в знаменатель формулы (4.13), получим уравнение описывающее вращение материальной точки под действием силы:

Угловое ускорение материальной точки равно отношению момента действующей на нее силы к моменту инерции точки относительно оси вращения.
Дата добавления: 2015-11-28; просмотров: 1280;
