Осьовий і полярний моменти опору
Ці найважливіші геометричні характеристики будемо називати похідними, тому що вони визначаються через уже відомі моменти інерції й формально вводяться у вигляді

| (10) |
де 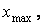
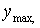
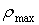 — відстані від осей y, x і центра координат до найбільш вилучених від них точок перетину відповідно;
— відстані від осей y, x і центра координат до найбільш вилучених від них точок перетину відповідно;
У відповідності з (6), всі ці величини виміряються в 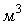 (система СИ) або
(система СИ) або 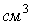 (розмірність, зручна для практичних розрахунків).
(розмірність, зручна для практичних розрахунків).
Моменти інерції при крутінні й моменти опору крутінню
Найчастіше крутінню піддаються стрижні круглого перетину (вали). У цьому випадку відповідні геометричні характеристики перетини називаються полярним моментом інерції й полярним моментом опору (про що вже було сказано вище) і обчислюються по формулах
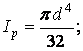 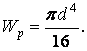
| (11) |
Якщо ж вали є порожніми, то
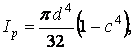 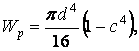
| (12) |
де c = d / D; D — зовнішній діаметр вала; d — внутрішній.
У той же час в інженерній практиці зустрічаються випадки, коли крутінню піддаються стрижні некруглого поперечного перерізу. Відповідні геометричні характеристики називаються моментом інерції при крутінні 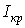 й моментом опору при крутінні
й моментом опору при крутінні 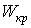 . Найчастіше доводиться зіштовхуватися із крутінням стрижнів прямокутного або квадратного перетину, тоді
. Найчастіше доводиться зіштовхуватися із крутінням стрижнів прямокутного або квадратного перетину, тоді 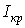 й
й 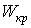 визначаються по формулах
визначаються по формулах
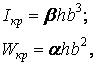
| (2.13) |
де 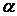 й
й 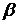 — коефіцієнти, що залежать від відношення h до b, і визначені відповідно до табл.2.1.
— коефіцієнти, що залежать від відношення h до b, і визначені відповідно до табл.2.1.
| Таблиця 2.1 |
| h / b | 1,5 | 1,75 | 2,0 | 2,5 | 3,0 | 4,0 | 6,0 | 8,0 | 10,0 | 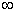
| |
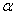
| 0,208 | 0,231 | 0,239 | 0,246 | 0,256 | 0,267 | 0,282 | 0,299 | 0,307 | 0,313 | 0,333 |
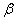
| 0,141 | 0,196 | 0,214 | 0,229 | 0,249 | 0,263 | 0,281 | 0,299 | 0,307 | 0,313 | 0,333 |
Дата добавления: 2016-01-26; просмотров: 2000;
