Моменти інерції однорідних тіл
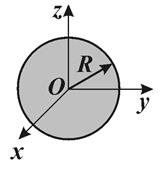
Диск у площині 
| 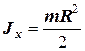
| 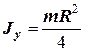
| 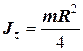
|
Прямокутник у площині 
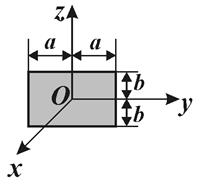
| 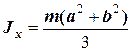
| 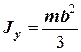
| 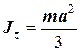
|
Куля

| 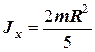
| 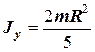
| 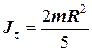
|
Тонкий стрижень
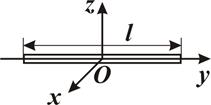
| 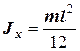
| 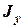 = 0 = 0
| 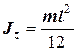
|
Для сукупності паралельних осей обертання момент інерції твердого тіла має мінімальне значення 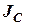 для тої осі, яка проходить через центр маси твердого тіла. Тоді для будь-якої іншої, паралельної до неї, момент інерції можна визначити за теоремою Гюйгенса-Штейнера
для тої осі, яка проходить через центр маси твердого тіла. Тоді для будь-якої іншої, паралельної до неї, момент інерції можна визначити за теоремою Гюйгенса-Штейнера
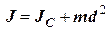 , (6.11)
, (6.11)
де  – маса тіла, а
– маса тіла, а 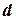 – відстань між центром маси тіла та віссю обертання
– відстань між центром маси тіла та віссю обертання
(рис. 6.2).
Можна довести теорему: похідна за часом від вектора моменту імпульсу механічної системи відносно даного центра  дорівнює головному моменту
дорівнює головному моменту 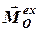 зовнішніх сил відносно того ж центра
зовнішніх сил відносно того ж центра
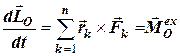 . (6.12)
. (6.12)
Формула (6.12) є математичним записом теореми про зміну моменту імпульсу механічної системи в диференціальній формі і називається також основним рівнянням обертального руху.
Векторне рівняння в проекціях на нерухомі вісі декартових координат еквівалентне трьом скалярним рівнянням
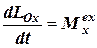 ,
,  ,
, 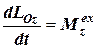 . (6.13)
. (6.13)
З наведеної теореми випливають наступні наслідки:
1) внутрішні сили безпосередньо не впливають на зміну моменту імпульсу механічної системи (вони можуть здійснювати опосередкований вплив через зовнішні сили);
2) якщо головний момент зовнішніх сил відносно деякого нерухомого центру дорівнює нулю, то момент імпульсу механічної системи відносно того ж центра не змінюється. Дійсно, якщо 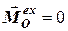 , то з рівняння (6.12) матимемо
, то з рівняння (6.12) матимемо
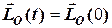 =
= 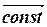 , (6.14)
, (6.14)
де 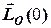 – початкове значення вектора
– початкове значення вектора 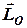 . Формула (6.14) є першим інтегралом рівняння руху системи і математичним записом закону збереження моменту імпульсу механічної системи;
. Формула (6.14) є першим інтегралом рівняння руху системи і математичним записом закону збереження моменту імпульсу механічної системи;
3) якщо головний момент всіх зовнішніх сил не дорівнює нулю, але його момент відносно деякої вісі (наприклад, 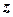 ) дорівнює нулю, то момент імпульсу механічної системи відносно цієї вісі не змінюється з часом. Дійсно з рівнянь (6.13) – (6.14) випливає, що коли, наприклад,
) дорівнює нулю, то момент імпульсу механічної системи відносно цієї вісі не змінюється з часом. Дійсно з рівнянь (6.13) – (6.14) випливає, що коли, наприклад, 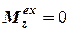 , то
, то
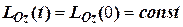 , (6.15)
, (6.15)
тобто зберігається відповідний компонент моменту імпульсу механічної системи;
4) якщо момент зовнішніх сил відносно нерухомого центру не дорівнює нулю, то з рівняння (6.12) отримуємо
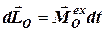 . (6.16)
. (6.16)
Після інтегрування (6.16) в межах від початкового моменту часу 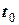 до поточного
до поточного 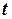 , отримуємо
, отримуємо
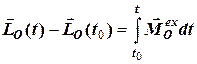 , (6.17)
, (6.17)
де 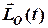 – момент імпульсу механічної системи на поточний час
– момент імпульсу механічної системи на поточний час 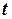 , а
, а 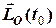 – в момент часу
– в момент часу 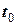 . Таким чином, зміна моменту імпульсу механічної системи відносно нерухомого центру
. Таким чином, зміна моменту імпульсу механічної системи відносно нерухомого центру  за проміжок часу від
за проміжок часу від 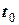 до
до 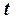 дорівнює інтегралу від головного моменту імпульсу зовнішніх сил по часу за той самий проміжок часу.
дорівнює інтегралу від головного моменту імпульсу зовнішніх сил по часу за той самий проміжок часу.
Формула (6.17) є математичним записом теореми про зміну моменту імпульсу механічної системи в інтегральній формі.
Контрольні запитання
1. Що характеризує момент імпульсу матеріальної точки?Як його знайти?
2. В яких випадках момент імпульсу матеріальної точки дорівнює нулю?
3. Як знайти момент імпульсу механічної системи?
4. Як знайти момент імпульсу твердого тіла відносно заданої осі?
5. Що таке момент інерції твердого тіла? Що він характеризує? В яких одиницях вимірюється?
6. Як формулюється теорема Гюйгенса-Штейнера?
7. Сформулюйте теорему про зміну моменту імпульсу механічної системи.
8. Чи можуть внутрішні сили змінити момент імпульсу механічної системи? Чому?
9. В яких випадках моменту імпульсу механічної системи зберігається?.
Дата добавления: 2015-12-10; просмотров: 1224;
