Теорема про рух центру мас механічної системи
Механічною системою називається сукупність матеріальних точок, положення та рух кожної з яких залежить від положення та руху всіх останніх. Зауважимо, що довільне матеріальне тіло можна розглядати як механічну систему, що складається з неперервної сукупності матеріальних точок.
Нехай механічна система складається з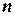 
матеріальних точок. Ці точки взаємодіють між собою внутрішніми силами 
(це сили, що діють на точку 
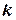збоку точки 
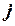). Крім того, на кожну з них діють зовнішні сили з силою 
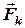.з боку тіл, що не входять в систему,
Основними властивостями внутрішніх сил є наступні:
= 
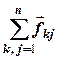= 0, 
, (4.1)
- векторна сума внутрішніх сил системи (головний вектор внутрішніх сил системи) дорівнює нулю, та
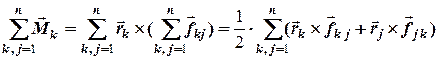= 0, , (4.2)
- векторна сума моментів внутрішніх сил системи (головний вектор моменту внутрішніх сил системи) відносно довільної точки дорівнює нулю.
Коли нам достатньо знати окремі параметри, які характеризують рух системи в цілому, в теоретичній механіці використовують ряд теорем.
Теорема про рух центра мас. Для системи, яка складається з 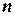матеріальних точок, положення центра мас механічної системи (радіус-вектор 
) визначається виразом
= 
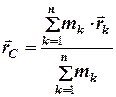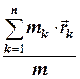, (4.3)
де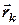 
– радіус-вектори матеріальних точок, що входять до системи, 
- маса системи.
Можна довести теорему: центр мас механічної системи рухається як вільна матеріальна точка, маса якої 
дорівнює сумі мас всіх елементів системи і на яку діє сила, що дорівнює головному вектору 
зовнішніх сил
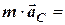
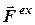= . (4.4)
тут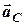 
– прискорення центра мас.
Векторне рівняння (1.2) еквівалентне трьом скалярним:
, 
, 
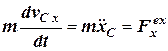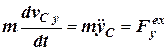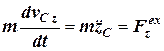, (4.5)
в яких 
, 
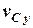та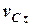 
– компоненти вектора швидкості центра мас, а 
, 
та 
– координати центра мас.
З наведеної теореми випливають наступні наслідки:
1) внутрішні сили не змінюють характер руху центру мас системи;
2) якщо головний вектор зовнішніх сил дорівнює нулю, то центр мас системи рухається рівномірно та прямолінійно, або знаходиться в стані спокою, тобто
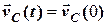, (4.6)
де 
– початкова швидкість центра мас. Якщо = 0, то
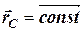, (4.7)
тобто центр мас системи не змінює свого положення в просторі;
3) якщо проекція головного вектора зовнішніх сил на деяку нерухому вісь (наприклад,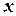 
) дорівнює нулю, то проекція швидкості центра мас системи на цю вісь не змінюється( 
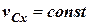), і якщо 
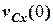= 0, тоді
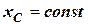, (4.8)
тобто центр мас системи не змінює свого положення в відносно осі .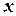
Контрольні запитання
1. Що таке механічна система? Наведіть приклад.
2. Які сили називають внутрішніми силами? Вкажіть їхні основні властивості.
3. Які сили називають зовнішніми силами?
4. Як визначається положення центра мас механічної системи?
5. Сформулюйте теорему про рух центра мас механічної системи.
6. При яких умовах центр мас системи знаходиться в стані спокою?
7. Чи можуть внутрішні сили змінити положення центра мас механічної системи?
Дата добавления: 2015-12-10; просмотров: 920;