Лекція 4 . Системи основних координатних переміщень. Поняття однорідних координат
4.1. Система основних координатних переміщень
До основних координатних переміщень належать усі орієнтуючі рухи механічної системи і додаткові переміщення ПР без урахування рухів захвату.
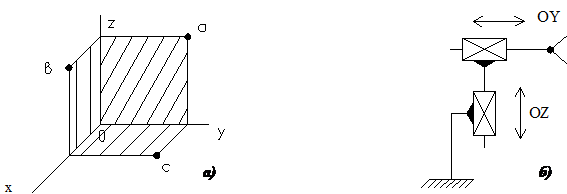 |
Система координат буває плоска й просторова. На рисунках.1, 3, 6 зображені відповідно прямокутна, полярна й ангулярна (кутова) плоскі системи координат, а на рисунках.2, 4, 7, 8 – прямокутна, циліндрична, сферична, ангулярна циліндрична й ангулярна сферична просторові системи координат. Там же наведені приклади структурних кінематичних схем ПР, що працюють у поданих на рисунках координатах, і форми робочих зон ПР без урахування обмежень координат (рис.4.1 – 4.4) і з їх урахуванням (рис.4.2 – 4.8).
Рис.4.1. Прямокутна плоска система координат (а); структурна кінематична схема ПР (б); форма робочих зон (а)
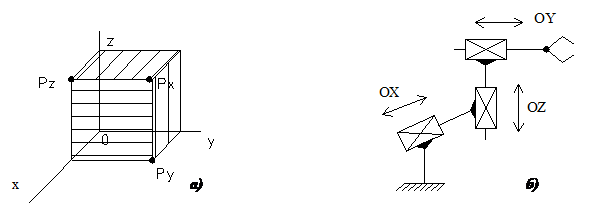 |
Рис.4.2. Прямокутна просторова система координат (а), структурна схема ПР (б_, форми робочих зон (а)
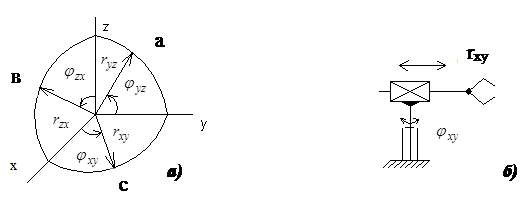 |
Рис.4.3. Полярна плоска система координат (а), структурна кінематична схема ПР (б), форми робочих зон (а)
 |
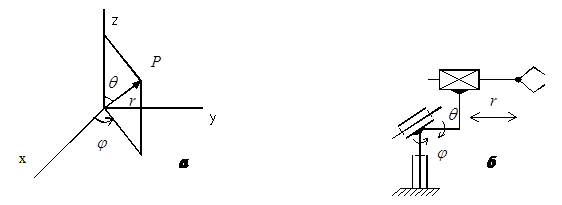 |
Рис.4.4. Полярна циліндрична система координат (а), структурна кінематична схема ПР (б), форми робочих зон (а)
Рис.4.5. Полярна сферична система координат (а), форми робочих зон з урахуванням обмежень координат (б), структурна кінематична схема ПР (в)
 |
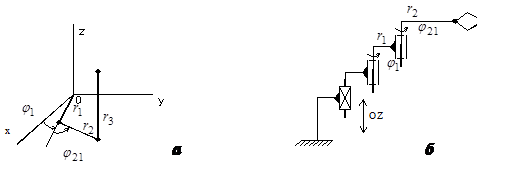 |
Рис.4.6. Ангулярна плоска система координат (а), форми робочих зон з урахуванням обмежень координат (б), структурна кінематична схема ПР (в)
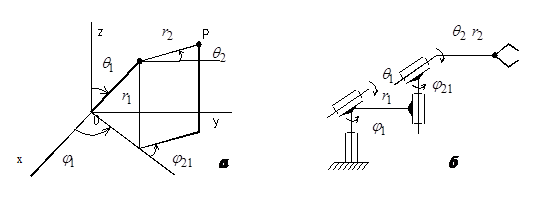
Рис.4.7. Ангулярна циліндрична система координат (а), форми робочих зон з урахуванням обмежень координат (б), структурна кінематична схема ПР (в)
Рис.4.8. Ангулярна сферична система координат (а), форми робочих зон з урахуванням обмежень координат (б), структурна кінематична схема ПР (в)
Системи координат розділяються на прямокутні й криволінійні. У прямокутних системах об’єкт маніпулювання переміщується тільки шляхом прямолінійних поступальних рухів ланок механічної системи ПР по двох (рис.4.1.) або трьох (рис.4.2) взаємно-перпендикулярних осях (0Х, 0У, 0Z). У криволінійних системах наявні обертальні рухи ланок механічної системи ПР відносно якої-небудь з осей 0Х, 0У, 0Z. Найбільш розповсюджена плоска (рис.4.3, 4.6), циліндрична (рис.4.4, 4.7) і сферична (рис.4.5, 4.8) системи.
У плоскій полярній системі (рис.4.3) переміщення об’єкта відбуваються в одній координатній площині х0у, у0z, z0х у напрямках вектора r або кута φ. У циліндричній системі (рис.4.4) об’єкт переміщується в основній координатній площині х0у в напрямках r i φ, а також по нормалі до неї в напрямку осі 0z. У сферичній (полярній) системі (рис.4.5) об’єкт маніпулювання переміщується в просторі за рахунок руху руки на величину r та її кутових переміщень φ і θ у двох взаємно перпендикулярних площинах.
Різновидами криволінійної системи є плоска ангулярна (рис.4.6), просторово–циліндрична (рис.4.7) і сферична (рис.4.8) системи координат. У ангулярній системі координат працюють багатоланкові шарнірні руки ПР та маніпуляторів.
В ангулярній плоскій системі об’єкт маніпулювання переміщується в одній з координатних площин, наприклад, х0у, як показано на рисунку.4.6, завдяки відносним поворотам ланок руки, що мають незмінну довжину.
Ангулярна циліндрична система характеризується додатковим зміщенням відносно основних координатних площин у напрямку, перпендикулярному до неї координатної осі (0z на рис.4.7).
В ангулярній сферичній системі координат переміщення об’єкта у просторі проходить тільки за рахунок відносних кутових поворотів ланок руки, при цьому хоча б одна ланка має можливість повороту на кути φ і θ у двох взаємно перпендикулярних площинах (на рис.4.8 обидві ланки можуть повертатися на кути φ і θ).
Розподіл відомих моделей ПР залежно від системи основних координатних переміщень у наш час:
– плоска прямокутна – 12%;
– просторова прямокутна – 8%;
– плоска полярна – 2,5%;
– циліндрична – 58,5%;
– сферична – 11%;
– ангулярна плоска – 0,5%;
– ангулярна циліндрична – 5%;
– ангулярна сферична – 2,5%.
Як видно з наведених даних, найбільша кількість моделей ПР працюють у сферичній системі координат, разом з цим в наступні роки спостерігається тенденція зростання числа конструкцій ПР, що використовують ангулярні системи координат.
4,2. Поняття узагальнених координат
Однорідними координатами деякої точки простору а декартової прямокутної системи координат 0xyz є будь-які чотири числа а1, а2, а3, а4, що одночасно не рівні нулю і задовольняють співвідношення: а4 ≠ 0; х = а1/а4; у = а2/а4; z = а3/а4.
Однорідні координати вводяться для зручності запису координатних перетворень. Вони дозволяють у єдиному виді записати як лінійні, так і кутові перетворення.
Основні операції над векторами, заданими в однорідних координатах, виконуються згідно з наступними правилами:
1. Додавання
А ± В = С,
де вектор С має координати 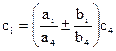 , причому с4 – будь–яке число, не рівне нулю; і = 1,2,3…
, причому с4 – будь–яке число, не рівне нулю; і = 1,2,3…
2. Множення на скаляр
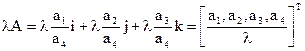 .
.
3. Модуль (довжина) вектора
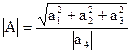 .
.
4. Скалярний добуток
 ,
,
де γ – кут між векторами А і В.
5. Векторний добуток
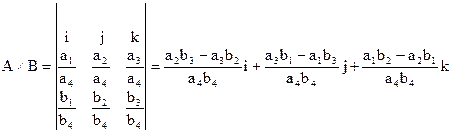 .
.
Звідси слідує, що однорідні координати вектору рівні:
с1 = а2b3 – a3b2; с2 = а3b1 – a1b3; с3 = а1b2 – a2b1; с4 = а4b4.
За допомогою однорідних координат можна задати будь-яку точку в просторі або лінію, наприклад (рис.1, а):
початок координат – (0,0,0,1);
вектор і (вісь 0х) – (1,0,0,0);
вектор j (вісь 0у) – (0,1,0,0);
вектор k (вісь 0z) – (0,0,1,0);
точка а (система 0xyz) – (3,4,5,1);
точка а (система 0/x/y/z/) – (6,8,10,2).
В однорідних координатах існує неоднозначність запису координати однієї і тієї ж точки у просторі, наприклад, точка а (рис.1,а), як записано вище, може бути визначена по-різному, що пов’язане зі зміщенням початку однорідних координат по всіх осях на відстань, рівну величині аі× (а4 = 1) (рівнозначне зміні масштабу рисунка).
Розглянемо координатні перетворення в загальному вигляді. Уявимо, що координати деякої точки а (рис.9) у однорідних координатах системи 0xyz описуються радіус-вектором А = [а1,а2,а3,а4]γ, тоді радіус-вектор А/ = [а1/,а2/,а3/,а4/]γ тієї ж точки у системі 0/x/y/z/ буде зв’язаний з першим співвідношенням:
а1/ = t11а1 + t12а2 + t13а3 + t1а4;
а2/ = t21а1 + t22а2 + t23а3 + t2а4;
а3/ = t31а1 + t32а2 + t33а3 + t3а4;
а4/ = а4.
Або у матричному вигляді
 ,
,
де Т – матриця лінійного перетворення координат від системи 0xyz до системи 0/x/y/z/.
Будь-яке перетворення координат може бути розбите на послідовні операції переносу вздовж і повороту навколо осей 0х, 0у, 0z. Матриця Т1 для лінійного переносу, наприклад, уздовж осі 0у на відстань ℓ2 має вигляд:
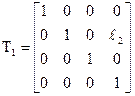 ;
; 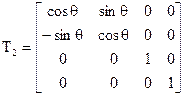
Відповідні координатні перетворення показані на рисунку.9,б.
На рисунку.9,в наведені координатні перетворення навколо осі 0z на кут +θ; відповідна такому перетворенню матриця має вигляд Т2.
Дата добавления: 2015-12-22; просмотров: 1910;
