Розв’язаня прямої задачі
Розглянемо розв’язання прямої задачі, виділивши три етапи розв’язання:
– визначення рівнянь зв’язку положення робочого органу маніпулятора з величинами узагальнених координат;
– визначення швидкості руху робочого органу як функції узагальнених координат і їх швидкостей;
– знаходження прискорення робочого органу як функції узагальнених координат, їх швидкостей та прискорень.
Для розв’язання прямої задачі зв’яжемо з основою робота систему координат 00x0y0z0, котра збігається з абсолютною системою, якщо основа нерухома, як на рисунку.1.; з першою ланкою систему 0xyz, положення якої визначається координатою першої ступеня рухомості; із другою – 01x1y1z1, положення якої відносно 0xyz, визначається другим ступенем рухомості і т.д.
Якщо деяку точку С у системі координат, зв’язаній з (і + 1)–ою ланкою, представити у вигляді радіус–вектора Сі+1, то між цим вектором та вектором Сі, що являє собою цю точку у системі координат, зв’язаній з і-тою ланкою, існує зв’язок
Сі = Т(і+1)і×Сі+1,
де Т(і+1)і – матриця перетворень координат із системи 0i+1xi+1yi+1zi+1 до системи 0ixiyizi.
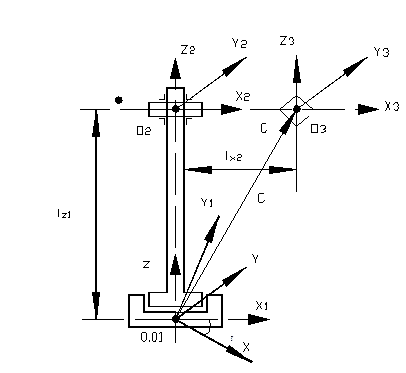 |
Рис.6.1. Координатні осі ПР, що працює в циліндричній системі координат
Матриці перетворення для рухів кінематичних пар V класу можуть бути записані в такому виді:
– для обертання навколо осі 0х:  ;
;
– для обертання навколо осі 0у:  ;
;
– для обертання навколо осі 0z:  ;
;
– для лінійного переміщення вздовж осі 0х: 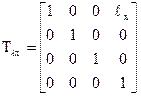 ;
;
– для лінійного переміщення вздовж осі 0у:  ;
;
– для лінійного переміщення вздовж осі 0z:  .
.
Знаючи положення робочого органу Сn у системі координат 0nxnynzn, що зв’язана з ним, можна знайти його положення С0 у абсолютній системі координат, яка зв’язана з основою робота або прив’язана до цехової системи координат за допомогою перетворення:
С0 = Т10Т21…Tn(n–1)Сn
Для будь-якої точки, заданої у і-й системі координат радіус-вектором Rі, цей вираз можна переписати у вигляді
R0 = ГіRі,
де Гі – Т10Т21…Ті(і–1) – матриця перетворення і-тої ланки, що описує її положення у системі координат 00x0y0z0.
Приклад
Для робота, що працює у циліндричній системі координат, розставимо сепаратні системи координат 0ixiyizi, як показано на рисунку.1. Центр захвату в системі координат 03х3у3z3, поміщений у його центр, описується радіус-вектором С3 = [0,0,0,1]Т. У системі координат 02х2у2z2, що зв’язана з 03х3у3z3 лінійним переміщенням руки ℓх2, координати центру ваги захвату визначаються, як С2 = Т32С3.
Перетворення виконується вздовж осі 02х2, отже,
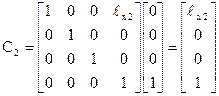
Система координат 02х2у2z2 зв’язана із системою 01х1у1z1 лінійним перетворенням по координаті ℓz1. Положення захвату С1 у системі координат 01х1у1z1 запишемо за допомогою лінійного перетворення С1 = Т21С2 або
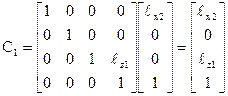
В абсолютній системі координат положення захвату визначиться, як С = Т10С1 або
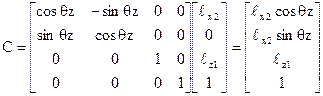
Аналогічні перетворення можна виконати і для кінематичної схеми робота, що працює у сферичній системі координат.
Дата добавления: 2015-12-22; просмотров: 842;
