Лекція 7 . Розв’язання зворотної задачі кінематики маніпулятора. Методи точного і наближеного розв’язання зворотної задачі
Розв’язання зворотної задачі кінематики для деякої ланки маніпулятора зводиться до розв’язання рівняння Сz = T32C3 відносно вектора узагальнених координат Q = [q1,q2, …qn]T.
Положення й орієнтацію захвату в системі координат, пов’язаній з основою робота, визначає матриця перетворення
Гn = T10T21…Tn(n–1) = 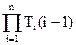 , (7.2)
, (7.2)
яке можна представити у вигляді
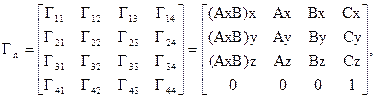 (7.2)
(7.2)
де С – вектор початку відліку системи координат 0nxnynzn, що зв’язана з центром захвату;
А – вектор орієнтації,
В – вектор підходу захвату,
АхВ – векторний добуток.
Розташування вказаних векторів показана на рисунку.1. Елементи матриці Гі визначають дванадцятимірний вектор-стовпець:
Хі = [Г11, Г12, Г13, Г14, Г21, Г22, Г23, Г24, Г31, Г32, Г33, Г34, Г41, Г42, Г43, Г44], (7.3)
що називається вектором положення і-тої ланки маніпулятора.
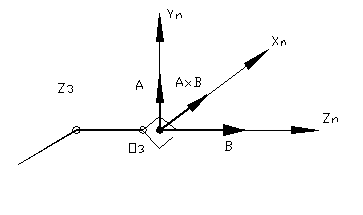 |
Рис.7.1. Розташування векторів підходу та орієнтування захвату маніпулятора.
Точний метод полягає у розв’язанні системи нелінійних рівнянь зв’язку заданого вектора Хізд положення у декартовій системі координат, зв’язан ій з основою робота, з вектором положення Хі(q) в узагальнених координатах:
Хізд = Хі(q),
що отримують шляхом прирівнювання аргументів вектора положення
Гjk.зад = Гjk(q); j = 1,2,3; k = 1,2,3,4. (7.4)
Гранично є дванадцять рівнянь зв’язку.
Точне розв’язання – у вигляді однозначних аналітичних залежностей узагальнених координат від геометричних параметрів маніпулятора і проекцій векторів А, В, С на осі системи 0xyz одержують на для всіх кінематичних схем. Наприклад, матриця перетворення для центра захвату маніпулятора, що працює у полярній сферичній системі координат, має вигляд:
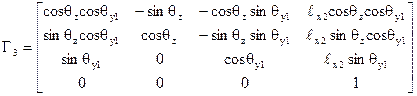 .
.
Оскільки в цьому прикладі розглянуто триступеневий маніпулятор, то для точного розв’язання зворотної задачі достатньо розв’язати систему з трьох рівнянь зв’язку відносно положення центра захвату в просторі (координат радіус-вектора С) Гjзд = Гj4(q), j = 1,2,3 у вигляді
 .
.
Розв’язок дає:
q1 = θz = arctg(Cyзд/Схзд),
q2 = θу1 = arctg 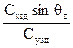 ,
,
q3 = ℓх2 = Cхзд/sinθy1,
Приклад
Нехай –180о ≤ θz ≤ 180о; –60о ≤ θу1 ≤ 240о; Схзд = 1м; Сузд = 1м; Сzзд = 0,817м.
Тоді: θz ≤ 45о або –135о; θу1 = 30о або 210о (θz = 45о), 150о або –30о (θz = –135о), ℓх2 = ±0,817/0,5 = ±1,634 м.
Розв’язок ℓх2 < 0 відкидається через абсурдність. Але неоднозначність розв’язку зберігається – є два правильних шляхи розв’язання (рис.2), один з котрих характеризується меншим кутом повороту першої координати (θz = 45o) і є оптимальним. При збільшенні числа ступенів рухливості маніпулятора, якщо рівняння зв’язку мають аналітичні розв’язання, зростає число допустимих розв’язків і вибір оптимальних з них може бути складнішим, ніж у розглянутому випадкові.
Гj4зд = Гj4(q).
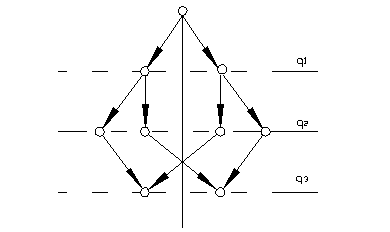 |
Рис.7.2. Граф вибору допустимих розв’язань зворотної задачі кінематики маніпулятора.
Наближені методи
Наближені методи дозволяють розв’язати зворотну задачу для будь-якої кінематичної схеми маніпулятора. Вона зводиться до численних розв’язань рівняння зв’язку Хізд = Хі(q).
Зворотна задача може розв’язуватися шляхом мінімізації функціоналу розузгодження:
І2(Q) = |Хзд – Х(Q)|2,
де Хзд – вектор положення у системі координат 00x0y0z0;
Х(Q) – вектор положення в узагальнених координатах, що функціонально залежить від вектора узагальнених координат Q = [q1,q2,…qi]T, і = 1,2,3,…n.
Мінімізація цього виразу, як правило, проводиться градієнтним методом із кінцевим кроком. Для цього треба у векторному просторі допустимих значень узагальнених координат Q вибрати можливі напрямок і крок зміни вектора Q при дотриманні умови Q € Q і побудувати послідовність Q[0], Q[1], …,Q[k], … Q[m], яка є мінімізуючою для функціоналі I2(Q), тобто
I2(Q[0]) > І2(Q[1]) >…> І2(Q[k]) > І2(Q[m]).
Процедура отримання цього виразу полягає, по-перше, із визначення координат вектора градієнта ∂I2(Q[0])∂qі і = 1,2,…,n.
Далі на першому кроці ітерації qi[0], і = 1,2,…n вибирають такі напрямки Δqi[1], щоб отримати переважно від’ємні значення вектора градієнта.
Потім на кожному кроку ітерації дають приріст Δqi[k], знаходять величину І2(Qi[k]) і перевіряють виконання послідовності. По мірі зменшення модуля градієнта зменшують величину кроку Δqi[k].
При неможливості або непрактичності визначення градієнта функціоналу переходять до кінцевих різниць ΔІ2(Q)/ Δqi. Почергово змінюють кожну координату та один крок ітерації виконується за n кроків.
Метод Ньютона
Широке застосування дістав метод Ньютона, згідно з котрим нелінійне рівняння зв’язку представляють у лінійному наближенні. Знаючи початкове значення координат qi[j], на кожному j–тому кроці ітераційного процесу шляхом розв’язання лінійних рівнязання знаходять наступне значення координат qi[j+1], що використовують як початкове для (j+1) - го кроку.
Дата добавления: 2015-12-22; просмотров: 997;
