Лекція 8. Динаміка механічної частини ПР. Динамічний аналіз. Складання рівнянь руху маніпулятора у загальних координатах
Під динамічним аналізом механічної частини ПР розуміють складання рівнянь руху маніпулятора. Скористаємося вивченим у курсі “Теоретична механіка” способом складання рівнянь руху за допомогою рівнянь Лагранжа ІІ виду.
У загальному випадку рівняння Лагрнажа ІІ виду записується так:
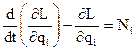 (8.1)
(8.1)
де L = Wк – Wп – функція Лагранжа, Wк – кінематична енергія системи, Wп – потенційна енергія системи, qі – і-та узагальнена координата,  і – швидкість і-тої узагальненої координати, Nі – і-та узагальнена сила.
і – швидкість і-тої узагальненої координати, Nі – і-та узагальнена сила.
Процедура складання рівнянь руху починається із знаходження узагальнених сил у механічній системі зі стаціонарними геометричними зв’язками з n ступенями свободи, що знаходяться під дією сил Fj (j = 1,2,…,m), прикладених у m точках. На основі викладених вище методів координатних перетворень для кожної j–тої точки прикладання сили можна знайти рівняння зв’язку в такому вигляді:
Rxj = fxj(q1,q2,…,qi);
Ryj=fyj(q1,q2,…,qi); (8.2)
Rzj = fzj(q1,q2,…,qi).
При максимально малих змінах (варіаціях) узагальнених координат δq1, δq2,…, δqn можливі переміщення точок j знаходяться як повні диференціали рівнянь зв’язку (функції fxj,fyj,fzj) від незалежних змінних q1,q2,…,qi.
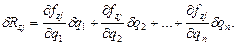 (8.3)
(8.3)
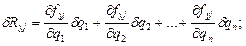 (8.4)
(8.4)
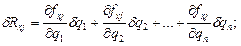 (8.5)
(8.5)
Тут доцільно зауважити, що можливим переміщенням цієї системи називається будь–яке елементарне переміщення, що допускається у даний момент накладеним на систему зв’язками.
Якщо необхідно позначити проекції сили Fj у j–тій точці на осі координат Fxj, Fyj, Fzj, то елементарна робота цієї сили в узагальнених координатах виразимо таким чином:
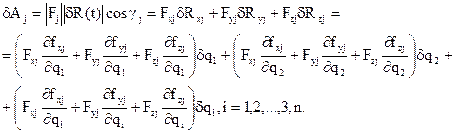
де δRj – вектор елементарного переміщення ланки у j-тій точці або варіація радіус-вектора δR(j) j-ї точки у вибраній системі координат.
γj – кут між вектором сили Fj, що прикладена до j-ї точки, і вектором δR(j).
Сума всіх елементарних робіт, що діють на систему сил, виражена у загальнених координатах, дорівнює:
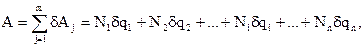
де узагальнену силу в і–тій координаті знаходимо
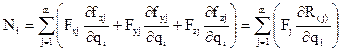
Узагальнені сили можна знаходити за цією формулою, а можна таким способом, що іноді більш зручний для розв’язання задач. Системі дається таке можливе переміщення, при якому тільки варіація однієї узагальненої координати не рівна 0 δqk ≠ 0, а усі наступні δqi = 0 (і ≠ k). При цьому визначаємо суму елементарних робіт усіх сил на цьому переміщенні 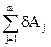 і беремо відношення
і беремо відношення
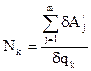 . (8.6)
. (8.6)
У загальному випадкові розмірність узагальненої сили не збігається із розмірністю сили. Так, елементарна робота моментів сил виражається у [Н×м×рад], варіації узагальненої координати в [рад] і N будуть мати розмірність моментів [Н×м].
Умовою рівноваги системи в узагальнених координатах, як слідує із рівняння Лагранжа, повинна бути рівність нулю всіх узагальнених сил, тобто сума елементарних робіт на всякому можливому переміщенні повинна дорівнювати нулю (приймають ідеальні зв’язки – без утрат).
Найбільш складним у процедурі складання рівнянь руху є вираз кінематичної енергії як функції узагальнених координат. Кінетична енергія системи в загальному випадку рівна сумі кінетичних енергій окремих ланок, що становить систему
Wк = ΣWкі,
Якщо вважати, що кожна наступна ланка робить просторовий рух, то його кінетична енергія може бути отримана як сума кінетичних енергій поступально рухомого центра мас і обертального руху ланки навколо цього центра.
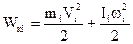
де mi – маса і-тої ланки, Vі – лінійна швидкість центра мас, ji – момент інерції і-тої ланки відносно осі обертання, що проходить через центр мас, ωі – абсолютна кутова швидкість навколо цієї ж осі.
Кінетична енергія деякої точки і-тої ланки масою dmі, що має радіус-вектор R, зв’язаний з початком координат абсолютної системи 0xyz, запишемо у вигляді:
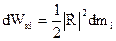
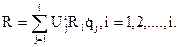
Квадрат модуля вектора швидкості можна знайти як скалярний добуток двох векторів швидкості – 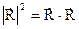
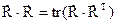 ,
,
де tr – слід матриці, рівний сумі її діагональних членів з однаковими індексами tr(A) = 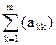 , RT – трансформована матриця швидкості, яка має вигляді:
, RT – трансформована матриця швидкості, яка має вигляді:
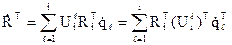
Підставивши 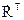 , отримаємо
, отримаємо

Кінетична енергія і–тої ланки рівна
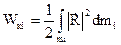
Підставивши сюди вираз для 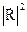 , отримаємо:
, отримаємо:
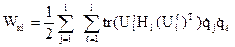
де Ні = 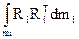 – матриця інерції і-тої ланки.
– матриця інерції і-тої ланки.
Отже, кінетична енергія системи визначається співвідношенням:
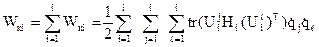 .
.
Потенційна енергія системи Wп створюється силами ваги ланок механічної системи, для і–тої ланки, масою mі вона дорівнює:
Wпі = migΔhі,
де g – прискорення вільного падіння, Δhі – висота підйому центра мас і–тої ланки.
Окрім сил ваги, слід ураховувати протидіючі їм сили механізмів урівноважування. Так, для пружин потенційна енергія сил пружності рівна:
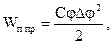
де Сφ – потсійна пружини, Δφ – кут її закручення.
Потенційна енергія маніпулятора в полі сил тяжіння при вертикально напрямленій осі 0z визначається співвідношенням:
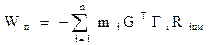 ,
,
де GТ = [0,0,g,0]Т – вектор прискорення вільного падіння;
Rіцм – радіус-вектор центра мас і-тої ланки у зв’язаній з ним системі координат.
Підставивши знайдені значення енергій у загальне рівняння Лагранжа і виконавши диференціювання, отримаємо рівняння Лагранжа ІІ виду для маніпулятора у явному вигляді:
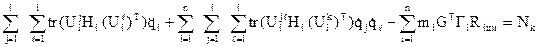
k = 1,2,…,n.
Дата добавления: 2015-12-22; просмотров: 1069;
