Моменти інерції деяких найпростіших перетинів

1. Півколо (рис.9).

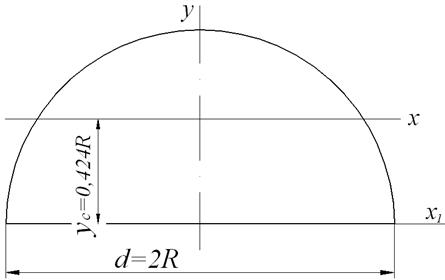
Рис.9. Перетин у формі півкола

Головними центральними осями є вісь симетрії у і перпендикулярна їй центральна вісь х. Зовсім очевидно, що момент інерції півкола вдвічі менше, ніж момент інерції кола щодо тої ж осі:

()

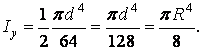
Таке ж значення має момент інерції щодо осі :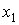

Скориставшись (2.8) і знайденим у прикладі 6.1 значенням ординати центра ваги півкола, одержимо

(14)

Якщо початок головних осей збігається з центром ваги перерізу, то осі мають назву головних центральних. У випадку наявності у фігури осей симетрією головні центральні осі збігаються з ними.

Визначимо моменти інерції круглого перерізу (рисунок 9')

;

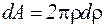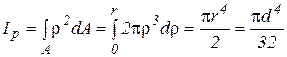. (15)

У нашому випадку

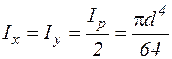. (15')

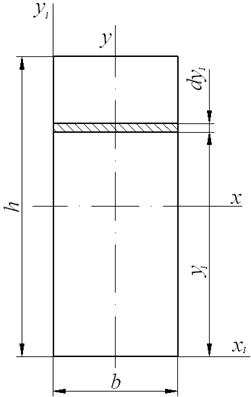
2. Прямокутник (рис. 10,а).

а	б

Рис.10. Прямокутний перетин

Визначимо спочатку момент інерції щодо осі, що збігає з основою.

По визначенню

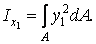
Розіб'ємо перетин на елементарні прямокутники (смужки) шириною 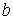й товщиною (висотою) 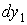, тоді Підставляючи значення 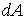у вираження для 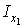й інтегруючи, одержуємо

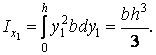
(16)

Головний центральний момент інерції знайдемо по формулі (8):

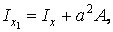
звідки

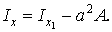
У цьому випадку відстань між осям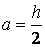и й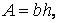

тоді

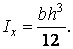
(17)

Аналогічно, момент інерції щодо осі у

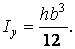
(18)

Для квадрата зі стороною 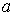на підставі (17)

(19)

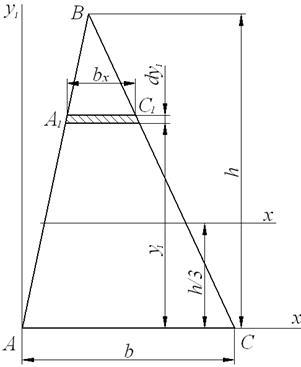
3. Трикутник (рис.10,б).

Обчислимо спочатку момент інерції щодо осі, що збігає з основою. Розбиваючи перетин на елементарні смужки, як показано на рис.10,б, знаходимо

Із подібності трикутників 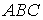і 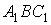одержимо

тоді

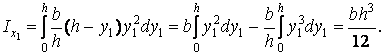
(20)

Підставляючи в (2.8) значення

,

знаходимо момент інерції щодо центральної осі :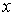

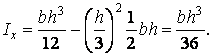
(21)

Для довільного трикутника вісь 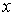не є головною; якщо ж трикутник рівнобедрений, то осі 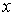й 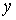головні, тому що вісь 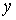є віссю симетрії.

Поняття про радіус і еліпс інерції

Момент інерції фігури щодо якої-небудь осі можна представити у вигляді добутку площі фігури на квадрат величини, яку називають радіусом інерції

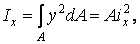
(22)

де 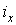— радіус інерції щодо осі .

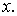З (22) треба, що

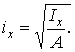
(23)

Аналогічно радіус інерції площі перетину щодо осі у

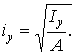
(24)

Головним центральним осям інерції 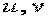відповідають головні радіуси інерції

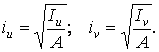
(25)

Побудуємо на головних центральних осях інерції фігури еліпс із півосями, рівними головним радіусам інерції, причому уздовж осі 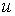відкладаємо відрізки 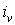, а уздовж осі — відрізки 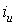(рис.2.15).

Рис.11. Еліпс інерції

Такий еліпс, що називають еліпсом інерції, має наступну властивість. Радіус інерції щодо будь-якої центральної осі 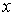визначається як перпендикуляр проведений із центра еліпса на дотичну, паралельну даної осі. Для одержання ж точки торкання досить провести паралельно даної осі 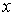будь-яку хорду. Крапка перетинання еліпса із прямої, що з'єднує центр О и середину хорди, і є крапка торкання. Вимірявши потім відрізок 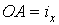,знаходимо момент інерції

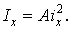
Запитання для самоконтролю

1. Перелічити та дати визначення основних геометричних характерис­тик поперечних перерізів бруса.

2. Як найбільш раціонально визначити координати центра ваги склад­ної плоскої фігури?

3. Як визначаються моменти інерції трикутника, прямокутника, круга?

4. Як змінюються моменти інерції в разі паралельного перенесення осей?

5. Осьові моменти інерції двох кругів відносяться як 16:1. Як відносяться їх площі?

6. Що розуміють під головними осями інерції?

Заняття № 46

Тема: Геометричні характеристики плоских перерізів.

План

1. Визначення головних центральних моментів інерції складних перерізів.

Студент повинен знати: визначення статичного, полярного, осьового моменту інерції поперечних перерізів, визначення осьових моментів інерції поперечних перерізів відносно параленьних осей, визначення головних центральних осей.

Студент повинен вміти:визначати статичний, полярний, осьовий моменти інерції поперечних перерізів складної форми.

ЛІТЕРАТУРА ОСНОВНА