Статичний момент площі. Центр ваги перетину

Розглянемо добуток елемента площі d на його відстань до осі x, а потім — до осі y. Підсумовуючи такі добутки для всього перетину, одержимо

,

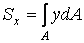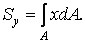
(2)

Величини, обумовлені формулами (2), є геометричними характеристиками поперечного перерізу й називаються статичними моментами площі щодо осей.

Очевидно, статичний момент має розмірність довжини в третьому ступені (виміряється в м³, см³, мм³).

Розглянемо той же перетин при паралельному переносі осей (рис.3):

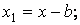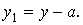
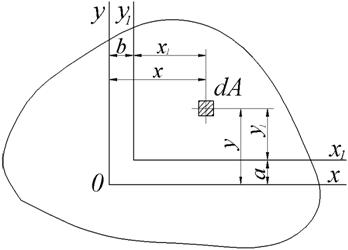
Рис.3. Паралельний перенос осей

По визначенню:

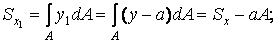
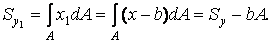
Очевидно, що величини a і b можуть приймати будь-які значення. Виберемо їх так, щоб виконувалися умови

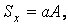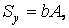
тоді

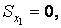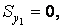
і осі 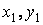називаються центральними осями, а точка їх перетинання — центром ваги перетину.

Отже, положення центра ваги перетину (точка З) визначається виразом

(3)

Залежно від положення осі, щодо якої обчислюється статичний момент, він може бути додатнім, від'ємним або рівним нулю.

З формул (3) випливає досить важливий наслідок: щодо будь-якої центральної, тобто минаючої через центр ваги, осі перетину його статичний момент дорівнює нулю.