Математическая модель мобилизующего отбора

Попробуем более формально проанализировать механизм действия мобилизующего отбора. Представим себе, что в какой‑то адаптивной зоне обитает большое число родственных видов, обладающих одним и тем же признаком – гомологичной и изофункциональной рабочей структурой. Пусть величина этого признака (под которым в данном случае мы понимаем логарифм мощности структуры) определяется суммарным вкладом его специальных генов. Каждый из них может находиться в двух аллельных состояниях 1 и 0. Аллель 1 соответствует активному состоянию гена (когда он экспрессируется), аллель 0 – отсутствию экспрессии. Таким образом, величина признака (Z) определяется числом специальных генов, находящихся в активном состоянии. Полное число генов (G) в геноме разных видов постоянно, тогда как число специальных генов (N ), определяющих степень развития признака, различно. Гены, не вошедшие в состав специальных (их число равно G – N ), будем называть «сторонними». Они определяют развитие каких‑то других (сторонних) признаков.

В среде обитания время от времени происходят медленные однонаправленные изменения, когда над каждым видом нависает реальная угроза гибели. Избежать вымирания вид может за счет компенсаторного изменения величины признака на какое‑то число единиц. (Что соответствует увеличению мощности рабочей структуры в какое‑то число раз.) Увеличение признака на одну единицу может произойти за счет фиксации мутаций двух типов. Во‑первых, это могут быть мутации, активирующие специальные гены, и, во‑вторых, мутации, переводящие ген из разряда «сторонних» в разряд специальных (с аллельным состоянием 1 ). Точно так же сдвиг признака в сторону его уменьшения может быть достигнут либо инактивацией одного специального гена, либо переводом активного специального гена в состав «сторонних».

Для своего филетического выживания каждый вид должен за единицу макроэволюционного времени осуществить фиксацию нескольких благоприятных мутаций (любого типа), изменяющих признак на требуемую величину ΔZ. Донорами этих мутаций являются чаще всего специальные гены признака, так как изменение экспрессии гена – более вероятное событие, чем его перепрофилирование. Соответственно вероятность филетического выживания вида (его адаптируемость) будет расти с увеличением числа специальных генов (N ). Это создает предпосылки роста генетической сложности признака.

Такая простая модель позволяет осуществить машинный эксперимент. На каждом шаге модели в окружающей среде каждого вида происходят случайные изменения, которые никак не связаны с изменением среды обитания остальных видов. От одних видов среда требует увеличения признака, а от других – уменьшения. Всю эту картину можно передать типом распределения величины ΔZ. В данном эксперименте мы остановились на биномиальном симметричном распределении. С подробностями вычисления вероятностей выживания видов в новых условиях среды можно ознакомиться в книге «Основные факторы макроэволюции».

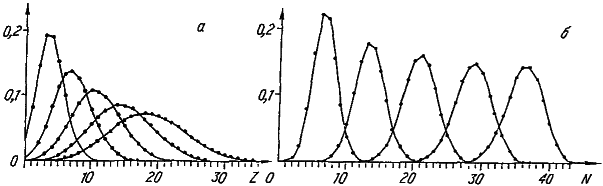
Рис. 27. Моделирование динамики видовых распределений по величине признака (а) и числу его специальных генов (б). Приведенные распределения (слева направо) соответствуют 20, 50, 100, 200, 800‑му шагу модели. Последнее распределение финальное.

Проследим за изменением видовых распределений по величине признака (рис. 27, а ). В начальный момент все виды обладают минимальным значением признака, поскольку его развитие обеспечивает всего один специальный ген. Однако завершается машинная эволюция широким финальным распределением со средним значением, равным 18,4. Таким образом, несмотря на то, что среда с равной вероятностью благоприятствует как увеличению, так и уменьшению значения признака, его средневидовая величина (<Z>) неуклонно растет. Правда, параллельно с этим нарастает и уровень межвидовых различий по степени развития признака (σ_z) (рис. 28). В итоге даже в финальном распределении после долгой эволюции сохраняется довольно много видов с «архаичной», «примитивной», величиной признака.

По‑иному ведет себя распределение видов по числу специальных генов (рис. 27, б ). По скорости роста среднего значения оно значительно опережает рассмотренное выше распределение по величине признака. Напомним, что рост числа специальных генов отражает усложнение генетической программы развития признака. Своеобразие динамики распределения видов по числу специальных генов состоит в том, что его размах стабилизируется гораздо раньше, чем среднее значение; поэтому в течение длительного отрезка времени мы наблюдаем практически параллельный снос вправо всего распределения. Следовательно, аккумуляция специальных генов идет со сходной скоростью во всех филетических линиях нашей эволюционирующей группы. Финальное распределение соответствует крайней специализации видов в отношении данного признака, поскольку большая часть генов генома попадает в разряд специальных (их среднее число равно 36,2). Ясно, что завершение процесса специализации обусловлено исчерпанием возможностей генома, число генов которого в данной модели неизменно (G=50).

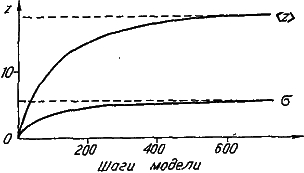
Рис. 28. Изменение среднего значения (<Z>) и сигмы (σ) распределений, представленных на рис. 27.

Так как мобильность признака определяется прежде всего числом специальных генов, то рост их среднего числа можно интерпретировать как рост мобильности признака. Мы видим, что модель вполне адекватно передает суть мобилизующего отбора.

Сравнивая оба типа финальных распределений (по N и по Z), следует отметить, что виды «архаичные» и «примитивные» в отношении величины признака оказываются вполне «продвинутыми» по его генетической сложности. Кажущаяся архаичность, очевидно, обусловлена низким уровнем экспрессии большинства специальных генов. Однако мобильность признака у этих «псевдоархаичных» видов довольно высока, поэтому, если начать эволюцию именно с них, финальное распределение достигается гораздо быстрее.

При сравнении данных модельных распределений с реальными распределениями аммоноидей по сложности сутуры нельзя не отметить их разительного сходства, которое распространяется даже на пропорциональность среднего значения и сигмы. Все это позволяет нам предположить, что сущность прогресса лопастной линии состояла в увеличении ее мобильности и, по‑видимому, эта цель была достигнута аммоноидеями к началу юры, когда они «освоили» все способы рассечения сутуры.