Отбор в панмиктической популяции

Перейдем к панмиктической популяции. Здесь при оплодотворении аллели гамет соединяются в генотипы зигот по правилам свободного попарного комбинирования. Зиготы с генотипами А₁А₁, А₁А₂ и возникают в соотношениях р²: 2pq: q² (рис. 10). Эти же соотношения, получившие название закона Харди‑Вайнберга, будут справедливы и для взрослых членов популяции, если приспособленность всех генотипов одна и та же. Закон Харди‑Вайнберга довольно часто выполняется в природных популяциях, он позволяет легко вычислять частоты генотипов, исходя из частот аллелей.

В нашей модели отличия в приспособленности особей обусловлены только разным уровнем их жизнеспособности, поэтому численности зигот трех генотипических классов А₁А₁, А₁А₂ и А₂А₂ соответственно равны Np ², 2Npq и Nq². Тем самым зиготы в точности отражают генофонд популяции взрослых особей предыдущего поколения. В результате действия отбора численности генотипов взрослых особей, развившихся из зигот, приобретают вид

N₁₁' = Np²w₁₁; N₁₂' = 2Npqw₁₂; N₂₂' = Nq²w₂₂ . (3.10)

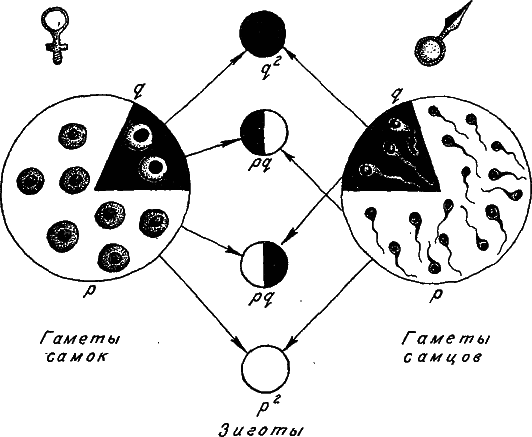
Рис. 10. Схема формирования генотипов зигот при случайном соединении гамет (при панмиксии).

Объяснения в тексте.

Численность всех взрослых особей после отбора связана с численностью зигот уравнением

N' = N(р²w₁₁ + 2pqw₁₂ + q²w₂₂). (3.11)

Поскольку отношение N'/N выражает среднюю приспособленность популяции (см. уравнения (3.8)), поделив обе части уравнения (3.11) на N, получим

w = р²w₁₁ + 2pqw₁₂ + q²w₂₂ . (3.12)

По аналогии с формулой (3.5) можно получить численность доноров аллеля А₂ после отбора, т. е. среди взрослых потомков

N₂' = N₂₂' + 0,5N₁₂' , (3.13)

или, учитывая соотношения (3.10),

N₂' = Nq²w₂₂ + Npqw₁₂ . (3.14)

Поделив обе части этого уравнения на N₂ = Nq (см. (3.6)), получим значение приспособленности доноров аллеля А₂ :

w₂ = N₂' / N₂ = (Nq(qw₂₂ + pw₁₂)) / Nq , (3.15)

т. е.

w₂ = pw₂₂ + qw₁₂ .

Точно так же можно показать, что

w₁ = pw₁₁ + qw₁₂ . (3.16)

Итак, мы располагаем всеми данными для вычисления сдвига частот аллелей после отбора (см. уравнение (3.9)).

Отбор в смысле Ч. Дарвина основан не на абсолютном уровне истребления молодых особей, а на различиях в степени такого истребления. В связи с этим приспособленность какой‑то группы особей удобно объявить равной единице, а приспособленность других групп представить в виде суммы 1 + s (s – коэффициент отбора). Такой прием позволяет рассмотреть наиболее интересную для нас задачу – судьбу мутаций, влияющих на относительную приспособленность их носителей.