Судьба вредной мутации

Предположим, что в огромной панмиктической популяции возник и каким‑то образом распространился новый аллель А₂ локуса А. (Ранее этот локус был представлен аллелем А ₁.) Ясно, что мутантный аллель может встречаться в гомо‑ и гетерозиготном состояниях. Если мутация вредная, значит, приспособленность гомозигот А₂А₂ должна быть ниже, чем у гомозигот по нормальному аллелю А ₁А ₁. Это обстоятельство мы можем отразить равенствами w₁₁ = 1, w₂₂ = 1–s. Возникает вопрос: какая приспособленность будет у гетерозигот А ₁А ₂?

В классической генетике рассматриваются три случая: 1) мутация рецессивна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по нормальному аллелю w ₁₂ = w ₁₁ = 1; 2) мутация доминантна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по мутантному аллелю w₂₂ = w₁₂ = 1–s; 3) случай неполного доминирования, когда приспособленность гетерозигот ниже, чем у гомозигот по нормальному аллелю, но выше, чем у гомозигот по мутантному. Степень доминирования можно оценить с помощью специальной величины А, варьирующей от нуля до единицы. При этом приспособленность гетерозигот можно выразить формулой w₁₂ = 1 – hs, охватывающей все три рассмотренных выше случая. При h = 0 мы имеем дело с рецессивной вредной мутацией, при h = 1 – с доминантной, а при неполном доминировании – 0 < h < 1.

Особый интерес для нас представляет случай полудоминирования, когда h = 0,5. Дело в том, что, по‑видимому, большинство вредных мутаций, постоянно возникающих в природных популяциях, полудоминантны. Приспособленности генотипов в этом случае определяются соотношениями

w₁₁ = 1; w₂₂ = 1 – s; w₁₂ = 1 – 0,5s . (3.17)

Эти равенства позволяют вычислять (с помощью формулы (3.12)) значение средней приспособленности популяции:

w = р² + 2pq(1 – 0,5s) + q²(1 – s) ,

или

w = (р² + 2pq + q²) – qs(р + q) .

Напомним, что p + q = 1, поэтому

w = 1 – qs . (3.18)

Аналогично с помощью уравнения (3.15) можно оценить приспособленность доноров мутантного аллеля:

w₂ = q(1 – s) + р(1 – 0,5s) = 1 – qs – 0,5ps . (3.19)

Теперь, подставив в уравнение (3.9) только что полученные значения для w и w₂ , получим сдвиг в частоте мутантного аллеля за одно поколение отбора:

Δq = ‑0,5(pqs / 1 – qs) . (3.20)

Так как мутация возникла недавно, то ее частота должна быть очень низкой. Если к тому же невелик и коэффициент отбора, то знаменатель правой части уравнения (3.20) мало отличается от единицы. Поэтому сдвиг частоты мутантного аллеля за одно поколение отбора можно оценить с помощью приближенной формулы

Δq ≈ ‑0,5pqs . (3.21)

Знак минус в правой части равенства указывает на то, что естественный отбор «стремится» снизить частоту аллеля A₂ . Эффективность этого отбора, получившего название очищающего, тем выше, чем выше частота мутантного аллеля и степень его вредоносности (s ).

Очевидно, что скорость появления в популяции мутантных аллелей пропорциональна частоте нормальных, из которых они возникают. Пренебрегая обратными мутациями, т. е. возникновением нормальных аллелей из мутантных, повышение доли аномальных аллелей за одно поколение можно оценить с помощью уравнения

Δq = vp, (3.22)

где v – мутабильность локуса, р – частота нормального аллеля.

В то же время очищающий отбор снижает частоту мутантных аллелей со скоростью 0,5pqs за поколение (где s – средний коэффициент отбора против вредных мутаций). Поскольку оба процесса – мутирование и отбор – противоположны по своему эффекту на приспособленность популяции, то должна существовать точка мутационно‑селекционного равновесия, когда поступление новых мутаций компенсируется их удалением из популяции очищающим отбором. Очевидно, в этой точке должно выполняться приближенное равенство

vp = 0,5pqs ,

откуда можно оценить равновесную частоту вредного аллеля q :

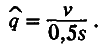
(3.23)

Эта частота прямо пропорциональна скорости появления вредных мутаций и обратно пропорциональна их среднему коэффициенту отбора. Поскольку природные популяции, несмотря на постоянно действующий процесс мутирования, не вымирают, то, очевидно, очищающий отбор со своей задачей успешно справляется. Между прочим, прямая оценка частот вредных мутаций в природных популяциях дрозофилы согласуется с уравнением (3.23).

Дрейф генов

Легко догадаться, что размер любой природной популяции не бесконечен хотя бы из‑за ограниченности пищевых ресурсов. Ясно, что колебания в интенсивности таких факторов, как хищники, болезни и т. д., должны отражаться на численности особей. Тем не менее популяция, обитающая в одной и той же местности в течение нескольких тысяч лет, способна сохранять свою численность на более или менее постоянном уровне. Чтобы лучше уловить идею генетического дрейфа, примем, что размер популяции неизменен. Мы знаем, что каждая особь способна произвести (и действительно производит) очень много гамет, которые после оплодотворения могли бы дать начало большому числу потомков. Постоянство размера популяции означает, что в среднем одна особь производит всего две гаметы, дающих начало взрослым особям следующего поколения. Иными словами, в основе формирования генофонда популяции потомков лежит выбор 2N гамет из гигантского по объему гаметного фонда родителей. Насколько полно аллели этих выбранных гамет отражают генофонд популяции?

При случайном выборе из гигантского гаметного фонда всего 2N гамет (пусть даже ровно по две от каждой особи) аллельные частоты в генофонде потомков обязательно отклонятся от их значений в генофонде родителей. Отметим, что при случайном выборе двух гамет из всех производимых одной гетерозиготной особью мы точно отразим ее генотип лишь в 50 % случаев. В остальных 50 % обе гаметы будут нести только один аллель, другой будет потерян.

Интуитивно ясно, что при уменьшении объема гаметной выборки падает точность, с которой она отражает аллельный состав генофонда родителей. Специальный анализ показывает, что наиболее вероятное (среднеквадратическое) отклонение (σ) частоты аллеля в обе стороны от исходной величины растет с уменьшением размера популяции, подчиняясь соотношению

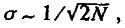
(3.24)

т. е. это отклонение обратно пропорционально квадратному корню из размера популяции.

Итак, на основании чисто статистических закономерностей частота каждого аллеля при смене поколений претерпевает сдвиг в совершенно непредсказуемом направлении. Этот феномен и представляет собой генный дрейф , его статистический характер не позволяет точно предсказать значения аллельных частот в популяции в ряду поколений. Более того, динамику изменения этих частот невозможно воспроизвести в принципе. Сколько бы раз мы ни следили за частотой какого‑то аллеля, мы никогда не встретимся с двумя одинаковыми его судьбами.

Особое значение генный дрейф приобретает в вопросе о судьбе аллелей, не различимых естественным отбором. Такие аллели принято называть селективно‑нейтральными или просто нейтральными. Сейчас мы увидим, что дрейф генов выступает как мощный фактор фиксации нейтральных аллелей. Проследим за динамикой частоты такого аллеля (A₁ ).

Пусть в популяции (будем считать ее популяцией нулевого поколения) исходная частота этого аллеля равна р₀ .

Предположим, у нас есть возможность очень много раз проследить за динамикой изменения частоты аллеля А₁ в большом ряду поколений. Тогда, определяя его частоту (р₁ ) в популяциях первого поколения, в каждой из них мы обнаружим отклонение от значения р₀. Поэтому частоту аллеля А₁ в любой из популяций первого поколения можно представить как р₀ + Δр (Δр – сдвиг частоты). Поскольку естественный отбор аллели не различает, вероятность изменения частоты аллеля А₁ в обоих направлениях одна и та же, т. е. среднее значение сдвига (где усреднение проведено по всем популяциям первого поколения) должно равняться нулю. Иными словами, средняя частота данного аллеля в совокупности популяций первого поколения <р₁ > должна в точности равняться его исходной частоте в нулевом поколении.

Так как направление сдвига частоты аллеля А₁ сохраняет свою полную неопределенность и в последующих поколениях, то средняя частота этого аллеля <р₂> в совокупности популяций второго поколения не должна отличаться от <р₁ >. Отсюда мы приходим к выводу, что в любом поколении средняя частота аллеля в совокупности популяций, происходящих от какой‑то одной, остается равной частоте этого аллеля в исходной популяции, т. е.

р₀ = <р₁> = <р₂> =… (3.25)

Несмотря на то что в каждой популяции динамика изменения аллельных частот непредсказуема, мы можем с полной уверенностью утверждать, что рано или поздно такие изменения прекратятся. Могут быть только два финала: или частота аллеля возрастет до единицы, или она опустится до нуля. Достижение нуля означает потерю аллеля, а достижение единицы – его фиксацию. На рис. 11 приведено несколько судеб нейтральных аллелей, смоделированных компьютером. Каждая траектория частоты аллеля заканчивается либо нулем, либо единицей. Случайный характер изменения аллельной частоты напоминает движение броуновской частицы в трубке, на концы которой помещено клейкое вещество. Очевидно, что при своем блуждании частица когда‑нибудь достигнет одного из концов трубки и там приклеится (зафиксируется). Итак, генный дрейф «стремится» уменьшить разнообразие аллелей, одна их часть теряется, а другая фиксируется.

Теперь рассмотрим совокупность всевозможных финалов частоты аллеля А₁ . У части финальных популяций она будет равна единице, а у всех других – нулю. Очевидно, что доля популяций, зафиксировавших в конце концов аллель А₁ (иначе говоря, вероятность фиксации данного аллеля), равна его средней частоте в полной совокупности финальных популяций. Поскольку (см. формулу (3.25)) последняя должна равняться частоте аллеля в исходной популяции (р₀ ), мы приходим к нетривиальному заключению: вероятность фиксации нейтрального аллеля равна его частоте в генофонде популяции. Например, если эта частота равна 0,5, то аллель с равной вероятностью может или исчезнуть из популяции, или в ней зафиксироваться. Теперь перейдем к очень важному следствию – к судьбе только что возникшей мутации.

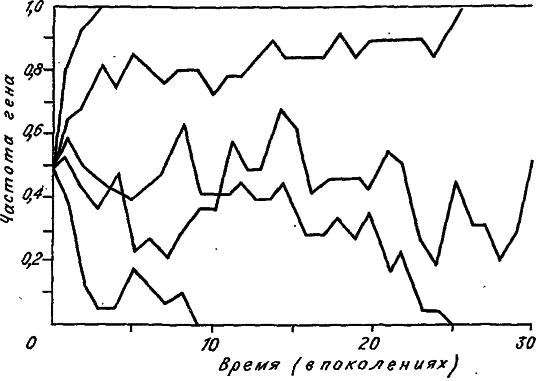
Рис. 11. Дрейф аллельных частот в пяти машинных экспериментах. Размер популяции N = 10. Исходная частота обоих аллелей 0,5 (по: [Kimura, 1983]).

Пусть в популяции возник совершенно новый нейтральный аллель. Очевидно, что его частота в момент возникновения равна 1/2N, поэтому и зафиксироваться с помощью дрейфа он может с той же вероятностью. Этот результат приводит нас к грустному выводу: фактически любой вновь возникший аллель обречен на исчезновение, поскольку вероятность этого события чрезвычайно близка к единице (1 – 1/2N ). В то же время заметим, что процесс мутирования постоянно ведет к появлению новых аллелей. Если через V обозначить мутабильность локуса, то в каждом поколении в популяции должно появляться 2NV мутантных аллелей. Поскольку они не различаются естественным отбором, любой из них может зафиксироваться с вероятностью 1/2N. Значит, в данном случае скорость фиксации любого мутантного аллеля только за счет генного дрейфа должна равняться 2NV(1/2N). Обозначив скорость фиксации мутантного аллеля через К, приходим к очень простому уравнению

K = V. (3.26)

Этот изящный результат, полученный М. Кимурой в 1960 г., показывает, что в популяциях (вне зависимости от их размеров) может идти процесс фиксации новых аллелей, скорость которого определяется только скоростью мутирования локусов. Однако среднее число поколений, нужное для фиксации мутантного аллеля с помощью дрейфа, пропорционально размеру популяции и, как показал Кимура, оно близко к 4N.

Заметим, что геном любого вида содержит несколько тысяч локусов, поэтому в генофонде любой популяции только вследствие неизбежного генного дрейфа почти в каждом поколении фиксируются какие‑то аллели. Однако подчеркнем, что этот вывод мы получили при допущении, что жизнеспособность организма не зависит от аллельного состава локусов; иными словами, естественный отбор эти аллели не различает. Несмотря на то что фиксация нейтральных аллелей занимает много времени, у данного процесса есть одна выгодная для популяции особенность – он проходит для нее совершенно бескровно.

Движущий отбор

До сих пор мы имели дело с панмиктической популяцией конечного размера, занимающей ограниченную территорию с фиксированными условиями среды. На самом же деле мир, в котором обитает популяция, изменчив, и идеально приспособиться к нему невозможно. Представим себе, что наша популяция в какой‑то момент времени хорошо приспособлена к условиям своего существования, однако вдруг эти условия начали медленно, но неуклонно ухудшаться. В данной ситуации перед популяцией встает проблема огромной сложности: нужно не просто отбраковать относительно редкие мутантные аллели (чему в немалой степени помогает генетический дрейф), но и заменить старые, далеко не дефектные аллели на иные, более благоприятные, т. е. лучше соответствующие новым условиям среды.

Будем считать, что благоприятные мутации полудоминантны, т. е. h = 0,5. Если принять приспособленность гомозигот по старому аллелю (w₁₁ ) за единицу, то приспособленность гомозигот по благоприятному аллелю (w₂₂ ) должна равняться (1+s ), а гетерозигот – (1+0,5s ). По аналогии с рассмотренным выше случаем вредных мутаций, заменяя – s на +s, можно рассчитать среднюю приспособленность популяции (w ) и среднюю приспособленность доноров благоприятного аллеля (w₂ ):

w = 1 + qs, (3.27)

w₂= 1 + 0,5ps + qs , (3.28)

тогда сдвиг частоты благоприятного аллеля за одну генерацию можно определить по формуле

Δq = (0,5pqs) / (1 + qs). (3.29)

При малых значениях q и s знаменатель в правой части этого уравнения мало отличается от единицы, поэтому с хорошей точностью должно выполняться соотношение

Δq ≈ 0,5pqs , (3.30)

т. е. скорость возрастания частоты благоприятного аллеля в генофонде популяции прямо пропорциональна его частоте и селективному преимуществу.

Глядя на соотношение (3.30), можно подумать, что были бы в наличии благоприятные мутации, а процесс их фиксации – дело десятое. Однако анализ решения этого уравнения показывает, что даже при таком высоком коэффициенте отбора, как 0,1, для достижения частот благоприятного аллеля, близких к единице, требуется около 100 поколений, при s = 0,01 – не менее 1000.

В этих оценках мы не учитывали ограниченность размера реальных популяций. Кроме того, мы полагали, что каждый носитель благоприятной мутации имеет все возможности реализовать свое селективное преимущество. На самом же деле, разбиение вида на небольшие популяции является весьма эффективным средством не столько для фиксации, сколько для удаления редких аллелей – как нейтральных, так и благоприятных.

Для того чтобы новый благоприятный аллель вытеснил старый, нужно еще и простое везение. К сожалению, мы сейчас убедимся, что шансы на такое везение не очень велики. Представим себе, что в популяции сколь угодно большого, но постоянного размера возник благоприятный аллель А₂. Его носителем может быть только гетерозигота А₁А₂ . Поскольку размер популяции постоянный, каждая особь передает в генофонд следующего поколения в среднем только две копии локуса А. Значит, гетерозигота А₁А₂ может передать эти две копии в виде одной из трех комбинаций: А₁А₁, А₂А₂ и А₁А₂. Первая комбинация означает потерю аллеля А₂, вероятность этого события равна 25 %. В 50 % случаев в генофонд следующего поколения будет передана только одна копия мутантного аллеля (и в следующем поколении он может снова с вероятностью 25 % потеряться), а в 25 % случаев количество мутантных аллелей удвоится.

В этом рассуждении мы не учитывали эффекта статистического варьирования числа потомков каждого родителя. Точное решение задачи было получено выдающимся английским математиком и генетиком Р. Фишером. Он продемонстрировал, что вероятность потери вновь возникшей нейтральной мутации в первом же поколении равна 0,37 и быстро растет с увеличением числа поколений, стремясь в конечном счете к единице. Если же мутантный аллель сообщает его носителю селективное преимущество s в гомозиготном состоянии и 0,5s в гетерозиготном, то вероятность его фиксации численно близка к s. Итак, если коэффициент отбора в пользу носителя одной копии благоприятного аллеля составляет целых 5 %, то все‑таки шансы его утратить равны 90 %. Следует заметить, что обычно s намного меньше единицы и даже меньше 0,1.

Положение может спасти лишь повторное возникновение благоприятных мутаций. Если скорость их возникновения равна v , то в популяции с размером N за одно поколение должно появляться 2Nv новых благоприятных мутаций, из которых будет фиксироваться доля, численно равная s. Отсюда скорость фиксации полудоминантных благоприятных мутаций (K ) определяется уравнением

К = 2Nvs . (3.31)

Заметим, что здесь v обозначает не скорость мутирования вообще, а только скорость возникновения благоприятных мутаций. Если среди всех возникающих за поколение мутаций (V ) благоприятные составляют долю f , то уравнение (3.31) можно слегка преобразовать:

К = 2NVfs . (3.32)

Эта формула хорошо передает особенность адаптивной эволюции. Ведь если число генов в геномах разных видов различается незначительно, то при приблизительном равенстве мутабильности локусов скорость адаптивной эволюции прямо пропорциональна доле благоприятных мутаций (среди всех возникающих) и средней степени их благоприятности. Если макроэволюция полностью сводима к микроэволюции, то уравнение (3.32) показывает, что для ускорения эволюции есть только два средства: увеличить селективное преимущество новых аллелей над старыми (s ) и, главное, повысить «выход» благоприятных мутаций (f ).

Плата за эволюцию

До сих пор мы рассматривали приспособленность как шансы зигот стать взрослыми организмами. Однако это понятие можно трактовать чуть‑чуть иначе. В популяции постоянных размеров каждая особь оставляет в среднем одного взрослого потомка. Если особи с каким‑то генотипом имеют повышенную или пониженную приспособленность, то это значит, что среднее число их потомков должно быть несколько больше или меньше единицы. Получается, что в популяции фиксированных размеров число взрослых потомков, оставляемых особью (ее мальтузианский параметр), может служить мерой ее приспособленности.

Мы знаем, что приспособленность популяции, в генофонде которой присутствует благоприятный аллель, за одно поколение немного возрастает, следуя за увеличением частоты данного аллеля. Но так как биомасса популяции увеличиться не может, то для сохранения прежней численности (в среднем один потомок на одного родителя) должно сократиться число потомков от обычных особей, не обладающих благоприятным аллелем. Иными словами, какая‑то часть популяции должна остаться без взрослых потомков, что с генетической точки зрения эквивалентно ее гибели (случай так называемой генетической смерти). Очевидно, что это падение относительной приспособленности должно компенсироваться увеличением мальтузианского параметра у носителей благоприятного аллеля.

Процесс фиксации благоприятного аллеля обычно занимает много поколений, и на каждом из них имеет место гибель определенной доли популяции. Просуммировав эти доли по всем поколениям (с момента появления аллеля до его фиксации), можно получить величину так называемой платы за эволюцию. Количественную оценку этой суммы дал в 1957 г. знаменитый английский ученый‑энциклопедист Дж. Холдейн. Он продемонстрировал, что плата за фиксацию полудоминантного благоприятного аллеля равна ‑2lnq₀ (q₀ – начальная частота аллеля). Иными словами, эта плата не зависит от коэффициента отбора, имеет значение лишь исходная частота благоприятного аллеля.

Если размер популяции равен миллиону особей, то частота благоприятного аллеля в момент его возникновения (1/2N) должна быть равна 0,5 * 10^‑6. Удвоенный натуральный логарифм этой величины равен примерно 29, т. е. для реальных популяций его можно принять равным 30. Заметим, что снижение средней приспособленности на единицу означает генетическую смерть (не надо смешивать ее с обычной смертью) всех особей популяции. Получается, что за фиксацию (с помощью отбора) одного аллеля популяция должна «заплатить» 30‑кратной генетической гибелью своих особей.

Это образное выражение совсем не следует понимать буквально. Биомасса эволюционирующей популяции остается на прежнем уровне, так как снижение относительной приспособленности носителей старого аллеля компенсируется повышением мальтузианского параметра у особей с благоприятным аллелем. Однако такое повышение не может превзойти возможностей особи к размножению – ее репродуктивного потенциала. Это обстоятельство ставит естественное ограничение на скорость адаптивной эволюции. Необходимость постоянно компенсировать генетическую гибель части популяции означает, образно выражаясь, увеличение нагрузки на репродуктивную функцию особей (во всяком случае, носителей благоприятного аллеля).

Теперь представим, что в популяции идет процесс фиксации сразу нескольких благоприятных аллелей. Ясно, что в этом случае плата за адаптивную эволюцию резко возрастает, что заставляет нас прийти к весьма пессимистическому выводу: популяция не в состоянии осуществлять параллельные адаптивные замещения аллелей сразу по нескольким локусам, поскольку дополнительная нагрузка на репродуктивный потенциал может превзойти возможности организма. Выходит, что благоприятные мутации скорее всего фиксируются популяцией не параллельно, а последовательно, т. е. адаптивная эволюция не может идти быстро.

Определенным выходом из «дилеммы Холдейна» могло бы явиться кооперативное, синергическое взаимодействие благоприятных мутаций. Подобное взаимодействие подразумевает, что две такие мутации повышают приспособленность больше, чем на простую сумму соответствующих коэффициентов отбора. В этом случае естественный отбор «хорошо видит» лишь комбинацию обоих мутантных генов и поэтому фиксирует их единым пакетом.

Генетический груз

В любой природной популяции всегда присутствуют вредные аллели, снижающие уровень ее приспособленности. Очищающий отбор «стремится» эти аллели удалить, но они снова появляются за счет вечно идущего процесса мутирования. Выше мы рассмотрели условия существования мутационно‑селекционного равновесия. Для полудоминантных мутаций их равновесная частота довольно низка. Если в каком‑то локусе скорость возникновения вредных мутаций равна 10^‑6, а s ~ 0,03, то равновесная частота вредящих аллелей в генофонде составит всего 6*10^‑5 (см.(3.23)). Казалось бы ничтожная доля, но ведь наше рассуждение подходит для всех локусов генома. Если это число равно 10 тысячам, то равновесная частота поврежденных аллелей при суммировании по всем локусам будет близка к 2/3. А если средняя скорость мутирования выше? Например, если средняя мутабильность локуса равна 10^‑5, то можно прийти к заключению, что в природных популяциях вообще отсутствуют особи без дефектных аллелей.

Исследования японского генетика Т. Мукаи, проведенные на дрозофиле, свидетельствуют в пользу именно этого предположения. Мукаи проанализировал спектр мутаций, снижающих жизнеспособность мух, и обнаружил, что большая их часть представлена полудоминантными мутациями, снижающими приспособленность всего на 2–4 %, остальные мутации рецессивны и снижают в гомозиготном состоянии жизнеспособность мух практически до нуля. Общая скорость возникновения слегка вредящих мутаций составляет около 0,4 на гаплоидный геном (т. е. на гамету) за поколение.

Заметим, что Мукаи оценивал лишь мутации, снижающие жизнеспособность, тогда как приспособленность должна включать и другие ее компоненты (например, плодовитость). В связи с этим реальное число повреждающих мутаций, возникающих в каждом поколении в геноме гаметы, может оказаться близким к единице (если не больше). При такой интенсивности мутирования можно уже подумать об уровне приспособленности популяции. Если мутантов не слишком много, то понижение производства ими потомков вполне может быть скомпенсировано усиленным размножением особей, лишенных генетических недостатков. Этих последних назовем для удобства элитой.

Различие между числом потомков у элиты и среднестатистической особи отражает так называемый мутационный генетический груз (L), смысл которого ясен из формулы

L = (w_э – w) / w_э , (3.33)

где w_э – средняя приспособленность генетической элиты. Фактически генетический груз показывает, во сколько раз особь из элиты превосходит по мальтузианскому параметру среднюю особь популяции.

Теперь снова вернемся к реальной ситуации, когда в среднем каждая гамета получает одну вредную мутацию. Как с этим может справиться очищающий отбор? Здесь может показаться, что положение совершенно безвыходное, поскольку все гаметы оказываются бракованными, и элите не из чего возникнуть. Однако дело спасает случайный характер мутирования.

Распределение мутаций по гаметам равносильно распределению капелек дождя по плиткам мостовой. Пусть дождь был слабым, и на одну плитку в среднем упала одна капля, но это не означает, что на каждую плитку попало в точности по одной капле. Ясно, что на некоторые плитки упали две, на иные три капли, а часть плиток вообще осталась сухой. В теории вероятностей такая ситуация хорошо описывается законом Пуассона. В соответствии с ним доля сухих плиток равна е^‑u. Здесь е – основание натуральных логарифмов, и – среднее число капель дождя, приходящееся на одну плитку. В нашем генетическом случае и – это число вредных мутаций, возникающее в среднем в одной гамете, поэтому доля гамет, счастливо избежавших мутаций, равняется е^‑u, а доля зигот, возникших от слияния бездефектных гамет, составляет е^‑2и. Отсюда следует, что для сохранения средней приспособленности популяции бездефектные особи должны размножиться в е^2и раз. В частности, при и = 1 каждая особь должна произвести не менее 7,39 потомков, что составляет довольно приличную нагрузку на репродуктивную способность элитных самок. А если эта величина еще больше?…

Однако вредные мутации могли бы удаляться не штуками, а сразу пакетами – по две, по три и т. д. Например, если вредная мутация рецессивна, то в гетерозиготном состоянии она не сказывается на приспособленности. Поэтому отбор «видит» только мутантную гомозиготу и, удаляя ее, освобождает генофонд сразу от двух экземпляров вредного аллеля. Если вредящий эффект мутации ощущается уже у гетерозиготы, то ее гибель унесет один вредный аллель, но заодно и один хороший. Следовательно, учитывая весьма широкое распространение слегка вредящих полудоминантных мутаций, природные популяции должны быть обременены весьма существенным генетическим грузом. Средством для его снижения мог бы быть кооперативный характер взаимодействия вредных аллелей разных локусов, когда вредящий эффект одной и той же мутации тем выше, чем больше подобных мутаций уже присутствует в геноме. При этом приспособленность особи по мере добавления мутаций падает по очень крутой параболе. Получается, что геном особи как бы накапливает вредные мутации, а при достижении какого‑то порогового значения происходит резкое падение приспособленности; особь с таким геномом гибнет, освобождая генофонд популяции сразу от нескольких вредных мутаций.

По мысли советского генетика А.С. Кондрашова, деление особей на два пола является специальным изобретением для снижения генетического груза. Его расчеты показывают, что половой процесс, резко увеличивая размах изменчивости особей по числу вредных мутаций, позволяет популяции гораздо эффективнее освобождаться от последних.

Главный вывод, который мы должны сделать после ознакомления с проблемой генетического груза, заключается в том, что среднее число вредных мутаций, возникающих в одной гамете за поколение, не должно превышать определенной фиксированной величины и* (которая является произведением средней мутабильности генов на их число в геноме). Скорее всего уровень спонтанного мутирования в природных популяциях близок к этой критической величине. В пользу такого предположения свидетельствуют две группы фактов. Во‑первых, скорость появления однотипных мутаций с качественным эффектом на фенотип у совершенно разных организмов довольно близка; во‑вторых, оценка числа жизненно важных генов (потеря которых ведет к прекращению развития) в геноме таких эволюционно далеких видов, как дрозофила и мышь, дает в обоих случаях близкие значения (5–10 тысяч генов).

Заметим, что наличие верхнего предела в скорости мутирования (u *) равносильно существованию ограничения на рост информационного содержания генома. Это обстоятельство часто не учитывается многими молекулярными биологами, которые считают, что количество наследственной информации можно оценить исходя из содержания ДНК в гаплоидном ядре.