Изменчивость особей

Вооружившись подходящим измерительным инструментом, мы можем убедиться, что взрослые особи любой природной популяции отличаются друг от друга по множеству характеристик (признаков): размерам тела и органов, частоте пульса, скорости бега, численности потомства и т. д. Попробуем найти способ, как оценить степень изменчивости популяции по таким мерным признакам.

Выберем наугад большое число особей (желательно одного возраста и пола) и измерим у них какую‑нибудь характеристику. Ясно, что в любой выборке можно найти одну особь с наименьшей величиной признака и одну – с наибольшей. Разность между этими значениями – диапазон варьирования мерного признака – может служить грубой мерой его изменчивости в популяции. Разобьем диапазон варьирования на ряд равных по величине интервалов. Очевидно, что с помощью этой процедуры мы разделим свою выборку на классы, каждый из которых формируется особями со значением признака, не выходящим за пределы соответствующего интервала. Теперь всю эту совокупность особей можно охарактеризовать ее распределением по признаку, т. е. числом особей, входящих в каждый класс. Фактически мы задаем тем самым математическую функцию численности особей от величины измеряемого параметра.

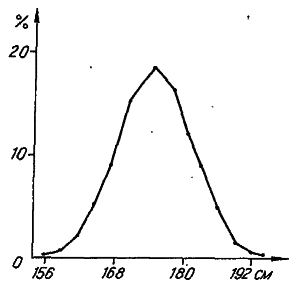
Рис. 13. Распределение студентов Гарвардского университета по росту (no: [Castle, 1916]).

Эту функцию удобно воспринимать графически (рис. 13). На оси абсцисс откладываем классовые интервалы, а ордината отражает численность особей, «приписанных» к соответствующему интервалу.

К настоящему времени изучены распределения по всевозможным признакам у большого числа популяций разных видов. Оказалось, что их графики обычно представляют собой непрерывные (гладкие) кривые с одной вершиной. Признаки, имеющие такие гладкие одновершинные распределения, в генетике принято называть количественными. Нередко графики этих распределений имеют симметричную колоколообразную форму, напоминая в этом отношении нормальное, или гауссовское, распределение, давно известное в теории вероятностей.

Центральным объектом теории вероятностей является так называемая случайная величина, которая характеризуется своим распределением, т. е. вероятностью принимать значения в заданных интервалах. В этой области математики доказывается, что нормальное распределение возникает, когда случайная величина является суммой большого числа независимо варьирующих, но близких по величине слагаемых. Классический пример представляет собой распределение ошибок, изученное великим немецким математиком К. Гауссом.

Вся информация о конкретном нормальном распределении заключена в двух его параметрах – среднем значении и дисперсии. Их можно легко вычислить и для нашей выборки особей. Среднее значение <x> – это просто среднеарифметическая величина признака. Угловые скобки обозначают операцию усреднения. Итак,

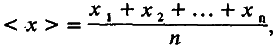
(4.1)

где х ₁, х ₂…, х _n – величина признака у первой, второй и т. д. особей; n – число особей в выборке.

Дисперсия распределения σ² отражает изменчивость особей по величине признака и является, по определению, средним квадратом отклонения величины признака от его среднего значения:

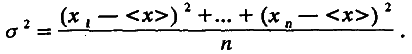
(4.2)

При получении распределения особей по признаку мы разбиваем всю выборку на n классов, каждый из которых может быть охарактеризован численностью и средним значением признака. Для удобства сравнения разных распределений вместо численности класса лучше взять долю , которую составляют его особи в выборке. Таким образом, i ‑й класс можно охарактеризовать его долей (р_i) в выборке и средним значением признака (х_i ). В этом случае среднее значение и дисперсия вычисляются по формулам

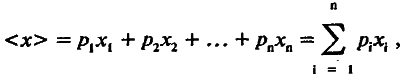
(4.3)

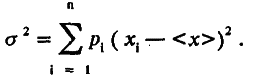
(4.4)