Ответ на искусственный отбор

Сначала рассмотрим, что кроется под таким образным понятием, как давление искусственного отбора. Проще всего под ним понимать долю отбракованных особей (I ), обычно измеряемую в процентах:

I = (N₀ / N) 100 %, (4.16)

где N – численность популяции до отбора; N₀ – число отбракованных особей. Недостаток формулы (4.16) состоит в отсутствии какой‑либо информации о признаке, по которому ведется отбор. Эту сторону работы селекционера передает так называемый селекционный дифференциал (S), который определяется как разница средних значений признака в исходной популяции (до браковки) (М ) и у «счастливцев», отобранных для развода (М_с), т. е.

S = M_c – M. (4.16)

Аналогично можно ввести представление об ответе популяции на отбор (R) как о сдвиге среднего значения популяции за одно поколение отбора:

R = M'_c – M , (4.18)

где M'_c – среднее значение признака у потомков «счастливцев».

Большой экспериментальный материал свидетельствует, что ответ на отбор прямо пропорционален селекционному дифференциалу. Следовательно, чем сильнее давление отбора, тем больше величина ответа на него. Величина этого ответа – внутреннее (генетически обусловленное) свойство популяции. Его количественной мерой является наследуемость – коэффициент пропорциональности (h² ), связывающий ответ на отбор с селекционным дифференциалом. Итак, при ответе конкретной популяции на отбор по конкретному количественному признаку выполняется равенство

R = h²S. (4.19)

Наследуемость разных признаков у особей одной популяции может существенно различаться. Кроме того, может различаться и наследуемость одного и того же признака в разных популяциях одного вида. Что же лежит в основе этого явления?

Пусть мы имеем дело с популяцией, состоящей из генетически идентичных особей. Многократно показано, что при любом давлении отбора среднее значение любого признака в следующем поколении практически не изменяется (h² = 0). Впервые это было продемонстрировано в знаменитом эксперименте В. Иогансена на чистых линиях фасоли. Иными словами, наследуемость равна нулю, если равна нулю генетическая компонента изменчивости.

Представим на момент, что мы в состоянии по фенотипу особи опознать ее генотип. Если к тому же эти особи размножаются бесполым путем, то состав генотипов потомков будет совпадать с таковым у отобранной группы родителей. Следовательно, и средние значения признаков потомков будут совпадать с их средними значениями у родителей, тем самым величина ответа на отбор сравняется с селекционным дифференциалом. Очевидно, что в данном случае h² = 1.

Обычно же ответ на отбор меньше селекционного дифференциала, так как часть особей попадает в отобранную группу совершенно случайно (вследствие счастливого стечения средовых факторов), поэтому особенность их фенотипа наследоваться не может. Ведь для того, чтобы потомки этих «баловней судьбы» (а не генотипа) попали в отбираемую группу, им снова должно повезти. Но случай на то и случай, чтобы не повторяться регулярно.

В генетике количественных признаков доказывается, что наследуемость равна доле генетической дисперсии в полной фенотипической дисперсии признака. Вспоминая, что эта последняя складывается из генетической и средовой компонент, сказанное можно передать формулой

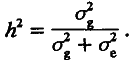
(4.20)

Повторяя процедуру отбора, направленного на изменение величины признака, в течение большого числа поколений мы можем в конце концов добиться фиксации генотипов, включающих в себя только сильные или только слабые аллели (в зависимости от направления отбора). Ясно, что в таком случае весь запас генетической изменчивости будет исчерпан, и дальнейший ответ на отбор станет невозможным.

Теперь обратимся к эксперименту. Действительно, у животных через несколько поколений отбора ответ на него обычно прекращается, и среднее значение признака выходит на плато. Однако интерпретировать это явление не так просто.