ПРЕДЪЯВЛЕНИЕ ОБУЧАЮЩЕГО МНОЖЕСТВА

Глава 3. ОБОБЩЕННАЯ ХАРАКТЕРИСТИКА ЗАДАЧ РАСПОЗНАВАНИЯ ОБРАЗОВ

Задачи распознавания образов характеризуются тремя основными факторами: способом, которым предъявляется наблюдателю обучающее множество, типом правила классификации образов, которое должен построить классификатор, и видом описания классифицируемых объектов [1]. Объединенные в трехмерную схему, эти три фактора условно изображены на рис. 6. Каждое ребро параллелепипеда представляет один из факторов, а ячейки внутри параллелепипеда соответствуют различным классам задач.

Рис. 6. Соотношение факторов в задачах распознавания образов

Например, ячейка «А» параллелепипеда на рис. 6 включает в себя те задачи, в которых процедура классификации образов должна вырабатываться на основе информации, содержащейся в единственной выборке, при условии, что каждый из объектов можно представить точкой в многомерном евклидовом пространстве описаний. Предполагается необходимость полного знания описаний объектов для определения правил классификации. В подобных задачах, для которых сохраняются евклидово пространство описаний и тип правила классификации, но относящихся к ячейке «В» (рис. 6), вместо классификации по единственной выборке используется последовательность выборок и коррекция правила классификации после каждой из них.

Три фактора, характеризующие задачи распознавания образов, далее будут рассмотрены более подробно, что необходимо для последующего анализа различных методов решения определенных классов задач.

ПРЕДЪЯВЛЕНИЕ ОБУЧАЮЩЕГО МНОЖЕСТВА

Различают процедуры распознавания образов, основанные на единственной выборке, и использующие последовательность выборок. В первом случае в результате наблюдения усеченной выборки ряда объектов из известных классов, предъявляемой системе распознавания образов до начала классификации, вырабатывается правило классификации, применяемое затем к объектам, которые предопределяются указанной выборкой, но в ней не содержатся. Сформированное таким образом правило далее не меняется, даже когда наблюдаются ошибки классификации. Во втором случае сформированное на основе анализа первоначальной выборки правило классификации применяется к следующей выборке, которая может состоять лишь из одного объекта. После анализа результата классификации, если возникает необходимость, отыскивается новое правило. Эта процедура повторяется до достижения некоторого критерия работы правила. Выработку процедуры классификации на основе фиксированной выборки обычно относят к статистике, а не к искусственному интеллекту. Разработаны соответствующие методы, особенно для задач на основе использования евклидова пространства описаний. Для экспериментальных исследований, где «классификация» проводится с данными, получаемыми при меняющихся экспериментальных условиях, важным вопросом является: обнаруживают ли члены, относящиеся к разным группам, систематические различия при измерении одной зависимой переменной?

Одна из наиболее изучаемых проблем искусственного интеллекта (машинного обучения) рассматривает случаи последовательной выборки. Непрерывное изменение правила классификации во многом аналогично способности большинства животных обучаться на опыте. Поскольку поступки животных считаются разумными по определению, система искусственного интеллекта также должна обладать подобной способностью к обучению.

В тех случаях, когда устройства распознавания образов обладают способностью обучаться путем приспособления своих правил классификации к последовательным выборкам, возникает задача оценки полезности и стоимости каждого изменения. Как правило, процесс изменения правил классификации является более трудоемким, чем классификация, использующая заданное правило. Так, врачи не могут изменять своидиагностические процедуры после обследования каждого больного, университеты не могут устанавливать новые правила приема в вуз каждый раз в зависимости от того, окончил данный студент университет или нет. Однако отсутствие возможности изменять ошибочное правило может привести к увеличению частоты ошибок классификации выше допустимых пределов. В экспериментальных исследованиях или в распознавании образов правила классификации обычно корректируют (изменяют) всякий раз, когда происходят ошибки, или в случаях превышения частотой появления ошибок некоторого допустимого уровня. Последнюю процедуру можно считать лучшим приближением к распознаванию образов в практических ситуациях.

Существуют устройства распознавания образов, в которых не учитывается информация об ошибках. В них для каждого класса наблюдается среднее значение по каждому сопоставляемому параметру, а новые объекты классифицируются на основании оценивания близости текущего значения этих параметров к среднему, которое в ходе эксперимента может также уточняться. Каждый раз, когда новый объект предъявляется для классификации, устройство распознавания получает дополнительную информацию об окружающей среде, использование которой в том числе позволяет корректировать оценки частоты появления объектов определенного типа. Существует два способа записи такой информации: последовательный и статистический. В первом информация о каждом объекте последовательно записывается в момент ее предъявления. Второй способ предполагает хранение обобщенной статистики, связанной с каждым классом и представляющей собой результат некоторого усреднения данных по всем наблюдавшимся до настоящего момента событиям в соответствующем классе. Примером может служить прогноз погоды, осуществляемый на основе представлений о «типичном» дождливом, пасмурном или ясном дне, которые корректируются по информации о текущих днях.

Существует несколько алгоритмов, эффективно отображающих множества всех возможных хранящихся в памяти записей о среде во множество возможных правил классификации, которые могут отличаться друг от друга аспектами, весьма существенными при их практической реализации. Наиболее существенными свойствами соответствующих процедур являются сходимость, оптимальность и вычислительная сложность.

Рассмотрим устройство распознавания образов, в котором первоначально используется произвольно выбранное правило классификации, а по мере получения информации путем демонстрации устройству объектов с указанием их классов вырабатывается последовательность новых правил классификации. Процедура сходится к окончательному правилу, если независимо от получаемой дополнительной информации устройство перестает строить новые правила. В оптимальном устройстве распознавания образов эта процедура минимизирует некоторую функцию стоимости ошибочной классификации, в качестве которой часто выбирается число ошибок классификации, однако она может быть и более сложной.

Существуют две важные разновидности понятия вычислительной сложности достижения результата: сложность собственно алгоритма распознавания образов, тесно связанная с вопросом сходимости, и сложность практического использования вырабатываемого им правила классификации.

ПРАВИЛА КЛАССИФИКАЦИИ. ВАРИАНТЫ ОПИСАНИЯ ОБЪЕКТОВ

Алгоритм распознавания образов, формирующий исходя из обучающего множества правило классификации образов, и тип используемого правила определяют процедуру распознавания. Существуют два общих метода классификации: параллельный и последовательный. В большинстве случаев объект можно описать при помощи вектора символов. В параллельной процедуре выполняется ряд тестов над всеми компонентами вектора, а затем делается предположение о принадлежности объекта классу на основе объединенного результата этих тестов. В процедуре последовательной классификации сначала проверяется некоторое подмножество компонент вектора описания, а затем в зависимости от результатов этих тестов или производится классификация, или выбирается новая совокупность тестов и новое подмножество компонент вектора описания, после чего указанный процесс повторяется.

Приведем формальные выражения для параллельной и последовательной процедур. Обозначим вектор описания объекта X = {x_i}, i = 1, …, n, и пусть объекты классифицируются в c классов. При параллельной классификации существует множество F = {f_j}, j = 1, …, c, функций не более чем n переменных. При реализации алгоритма классификации объект относится к классу j тогда и только тогда, когда

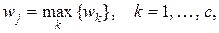(15)

где 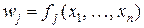для j = 1, …, с. Термин «параллельный» здесь оправдан, поскольку не важно, в каком порядке вычисляются функции f_j, и, значит, если только для этого есть возможность, они могут вычисляться одновременно. Время, затрачиваемое на классификацию, будет определяться наибольшим временем, необходимым для вычисления любой из функций f_j, хотя общее количество вычислительных ресурсов, требуемых для проведения классификации, равно сумме ресурсов, требуемых для вычисления каждой функции f_j .

В наглядном примере параллельной процедуры (Селфридж, 1959 г.) предполагается, что каждая функция f_j заменена маленьким демоном, задача которого – исследовать описание и выкрикивать название своего класса, если он считает, что объект относится именно к этому классу. Если демон уверен в своем решении, он должен кричать громко, и тихо, если не уверен. Общий шум будет зависеть не только от его стараний, но и от мощности его крика, которую оценивает «всемогущий» демон путем наделения демонов первого порядка сильным или слабым голосом. После предъявления классифицируемого объекта каждый демон выкрикивает название своего класса с интенсивностью, зависящей от его собственных оценок и от силы данного ему голоса. Демон, который ведет себя как председатель собрания, решает, название какого класса было выкрикнуто громче всех.

Процедуры последовательного решения, несколько более громоздкие в плане формального описания и реализации удобнее представить в виде дерева, указывающего порядок, в котором должны производиться тесты. На рис. 7 изображена часть дерева, соответствующая последовательной процедуре решения при постановке медицинского диагноза. Первый тест относится к самому верхнему узлу дерева; в зависимости от результата следующий тест выбирается из правого или из левого узла, соответствующего только что выполненному тесту. Название класса связывается с концом каждой ветви, например, узел «А» на рис. 7.

Последовательная процедура решения подвержена ошибкам в случае ненадежности отдельных тестов, как в смысле ненадежности устройства, их выполняющего, так и в том смысле, что каждая компонента x_j вектора описания определяется вероятностно при задании объекта. При возникновении ошибки в измерениях последовательная процедура может выбрать в дереве неверный путь, причем при этом нет возможности его исправить. В параллельной же процедуре ошибки измерения не столь опасны, поскольку рассматриваемая классификация будет зависеть от всех имеющихся результатов испытаний. Кроме того, из двух функционально эквивалентных вариантов последовательная процедура может оказаться существенно более продолжительной.

Способы описания объектов:

1) по набору измерений;

2) по списку признаков;

3) структурное описание.

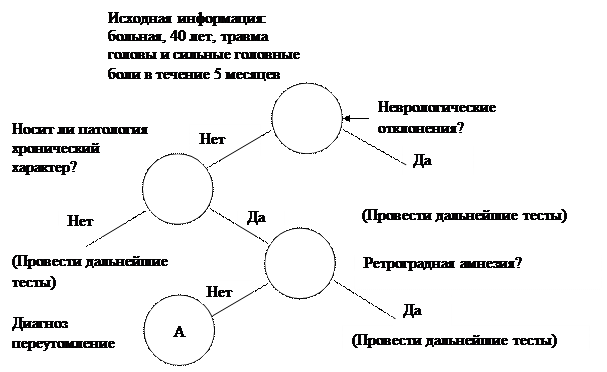
Рис. 7. Последовательная процедура решения при постановке
медицинского диагноза (кружки указывают путь классификации в
рассматриваемом случае)

Процедура описания путем набора измерений широко применяется в задачах классификации физических объектов. Этот подход основан на предположениях, что каждый классифицируемый объект можно описать совокупностью измерений, определяющих оси евклидова пространства, и что все измерения будут известны устройству классификации образов к моменту, когда должна производиться классификация. Результаты измерений определяют евклидово пространство описаний, в котором каждый объект представляется точкой, а сама классификация основывается на оценке близости (расстояния) этой точки к «типичной» точке, определяемой статистической обработкой результатов измерений для каждого класса объектов.

Во втором способе описание объекта – это список признаков, а не набор измерений. При этом имеющие смысл математические операции с векторами, соответствующими данному способу описания, будут совершенно другими.

Структурные описания объектов выделяют взаимоотношения между компонентами объекта, а не характеристики объекта, получаемые в серии измерений.