КЛАССИЧЕСКИЙ СТАТИСТИЧЕСКИЙ ПОДХОД К РАСПОЗНАВАНИЮ ОБРАЗОВ И КЛАССИФИКАЦИИ

Реализация байесовской процедуры классификации образов предполагает наличие априорной информации о вероятности появления события из некоторого класса и плотности распределения вероятностей описаний по пространству описаний для каждого класса. Поскольку во многих случаях эта информация отсутствует, проблема статистической классификации образов решается в предположении, что вероятности принадлежности классу соответствуют относительным частотам попадания выборок в различные классы, а распределение описаний по пространству для каждого класса оценивается некоторой приемлемой, заранее известной функцией

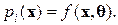(16)

Значения компонент вектора параметров q определяют по выборке, а затем применяется байесовская процедура классификации.

Рассмотрение метода статистического распознавания образов для
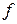– многомерного нормального распределения – можно оправдать следующими логическими соображениями. Допустим, что для каждого класса существует идеальный, или типичный объект. Пусть 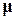– его вектор измерений (в шкале интервалов), который определяет в пространстве описаний точку, соответствующую идеальному члену некоторого класса. Выбранный из этого класса реальный объект будет иметь описание 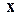, не обязательно совпадающее с 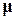. Любое отклонение 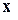от значения 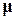может происходить, в частности, из-за воздействия определенных (возможно, небольших) отклонений каждого из измерений. В задаче классификации спортсменов по росту и весу на классы «баскетболисты» и «футболисты» можно предположить, что существует идеальный «тип баскетболиста», но любой конкретный игрок случайным образом отличается от этого типа по росту и весу. Отметим, что возможна корреляция отклонений по каждому измерению, например, если игрок выше обычного, он, по-видимому, будет и тяжелее. В рассматриваемом методе классификации такие корреляции в отклонениях от идеального типа будут учитываться. Для многомерного нормального распределения результатов наблюдения с центральной точкой 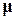в пространстве описаний D каждый класс i характеризуется следующими параметрами:

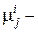среднее значение объектов в классе i при измерении j;

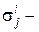среднеквадратическое отклонение в классе i при измерении j;

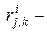коэффициент корреляции результатов измерений j и k для объектов из класса i.

Роль вектора 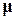, представляющего «идеальное» описание, играет вектор средних значений измерений объектов в выборке из класса i

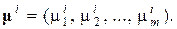
Если результаты некоторых экспериментов или наблюдений представить в виде матрицы, строки которой соответствуют различным наблюдаемым объектам, а столбцы – параметрам, описывающим состояние каждого объекта, то такая матрица называется матрицей данных. Обозначим число объектов через N, а параметров – через n. Тогда матрица данных Z имеет вид

Z = 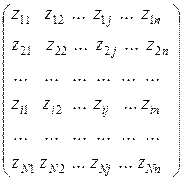. (17)

В этой матрице элемент 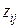указывает значение, которое принимает j-й параметр на i-м объекте.

Параметры, описывающие один и тот же объект, могут иметь различный физический смысл. Это приводит к тому, что матрица данных будет изменяться при изменении шкал, в которых измеряются те или иные параметры. Соответственно различные столбцы матрицы данных (т. е. различные параметры) оказываются трудно сопоставимыми между собой. Поэтому матрицу данных еще до проведения анализа приводят к стандартному виду, при котором средние значения всех параметров равны нулю, а дисперсии – одному и тому же числу. Такое преобразование можно понимать как приведение всех параметров к некоторой единой стандартной шкале.

В особых случаях, когда все параметры имеют одинаковый физический смысл и когда сама цель исследований заставляет нас принимать во внимание абсолютные значения параметров, преобразование данных не производится. Такая ситуация может возникнуть, например, при анализе различных поставок комплектующих предприятию, когда поставки всех комплектующих измеряются в рублях, т. е. в сопоставимых единицах.

Переход от матрицы Z к стандартизованной матрице данных
X = {x_ij} осуществляется следующим образом:

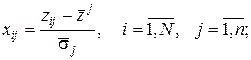
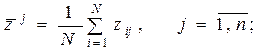(18)

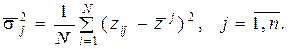
Элементы матрицы X обладают следующими свойствами:

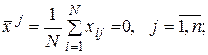
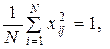(19)

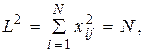
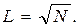
Эти свойства матрицы X и позволяют говорить о ней как о стандартизованной матрице данных. Геометрическую матрицу данных X можно иллюстрировать двояко. С одной стороны, можно рассматривать n-мерное пространство, оси которого соответствуют отдельным параметрам, а каждую строку матрицы X интерпретировать как вектор в этом пространстве. Такое пространство называют пространством параметров, а вся матрица X может быть представлена как совокупность N векторов в пространстве параметров.

С другой стороны, можно рассматривать N-мерное пространство, оси которого соответствуют отдельным объектам. Тогда каждый столбец x 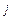матрицы X представляет собой вектор в этом пространстве, а матрица X – совокупность n таких векторов. Это пространство называют пространством объектов, которое удобно потому, что в этом пространстве все векторы x 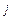имеют одинаковую длину , так что вопрос о взаимосвязи между параметрами очень часто сводится к оценке угла между соответствующими векторами в пространстве объектов.

Используя понятие коэффициента корреляции, матрице данных X размерности 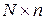поставим в соответствие квадратную матрицу коэффициентов корреляции или, как ее еще называют, корреляционную матрицу K размерности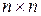

K 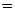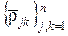, j, k =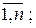

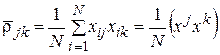. (20)

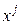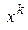Поскольку длины векторов и равны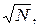

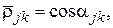
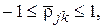
где 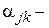угол в N-мерном пространстве между векторам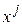и и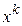

Корреляционная матрица K – симметрическая матрица, т. е. 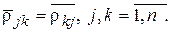На главной диагонали матрицы K стоят единицы,
т. е.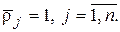

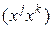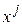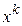Величины коэффициента корреляции, где – скалярное произведение двух векторов-столбцов и , являются показателем связи соответствующих параметров объектов между собой. Так, при значении 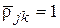векторы 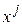и 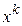полностью совпадают, т. е. эти параметры принимают одинаковые значения на любом из объектов, а при значении 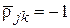имеем 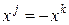. С уменьшением величины 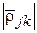в меньшей степени по значениям одного параметра можно предсказывать значения другого параметра, т. е. тем меньше связаны параметры 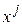и 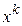между собой. Описанная ситуация в наглядной форме представлена на рис. 8. Как видно из условного изображения пространства N объектов, четыре параметра 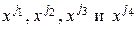расположены в нем так, что углы между ними соответственно равны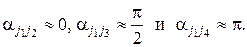

Таким образом, коэффициент корреляции является удобным показателем «близости» или «связи» параметров. Тем не менее «сильно связанные» параметры могут иметь в ряде случаев коэффициенты корреляции, равные нулю.

Матрица дисперсий для класса 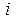представляет собой 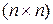– матрицу

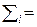
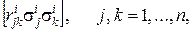(21)

где 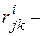коэффициент взаимной корреляции результатов измерений 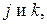вычисленный по объектам из класса i; 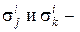среднеквадратическое отклонение в классе i при измерении j и k, соответственно.

С учетом автокорреляции каждого измерения диагональные элементы 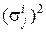матрицы S_i являются дисперсиями измерений, произведенных в классе i.

В простейшем случае, когда матрицы дисперсий для всех классов одинаковы, рассматривают одну матрицу дисперсий S с соответствующими элементами. Тогда многомерная нормальная функция плотности вероятности в пространстве 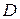для класса 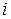имеет вид

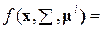
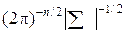
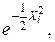(22)

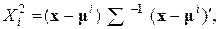
где 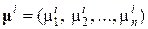– вектор средних значений параметров объектов в выборке из класса i; 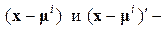исходный вектор-столбец и транспонированный, соответственно; |S| – определитель матрицы S.

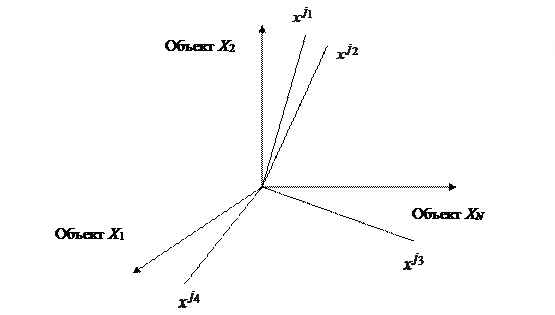
Рис. 8. Иллюстрация связи соответствующих параметров объектов;
оси N-мерного пространства соответствуют различным объектам

Не ограничивая общность рассуждений, рассмотрим вместо многомерных двухмерные измерения, так что пространство описаний будет плоскостью (рис. 9). Плотностьвероятности для класса в любой точке плоскости представим отметкой высоты в направлении, перпендикулярном плоскости. Каждый класс определяет «холм плотности», основание которого лежит на этой плоскости, при этом «холмы плотности» для различных классов могут перекрываться. Каждый холм на рис. 9 изображается линией одинаковой плотности подобно линиям на топографической карте. Для всех точек на такой линии вероятности 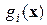принадлежать одному и тому же классу зависят как от вероятности 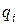того, что случайно выбранный объект принадлежит классу 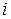, так и от относительной частоты элементов данного класса 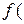x; 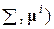в рассматриваемой точке 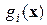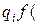x:

= x;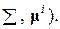

При многомерном нормальном распределении линии одинаковой плотности являются эллипсами с центральной точкой 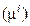, соответствующей максимальной плотности, т. е. вырожденным эллипсом, а плотность для рассматриваемой линии будет определяться наименьшим расстоянием от точки 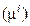до этой линии. Каждая линия одинаковой плотности будет окружать все линии с большей плотностью, и в свою очередь будет окружена линиями с меньшей плотностью. Картина эллипсов, соответствующих нескольким плотностям, отображает относительное расположение распределений для разных классов.

На рис. 9. показан случай двух классов, холмы плотности для которых ориентированы одинаково, хотя размеры их различны. Это вытекает из предположения о равенстве матриц дисперсий для обоих классов, поскольку именно матрицы дисперсий определяют ориентацию эллипсов. Точки на границе между областями R_i и R_j можно отнести классу i или к классу j, не изменив потери, вызванные ошибочной классификацией.

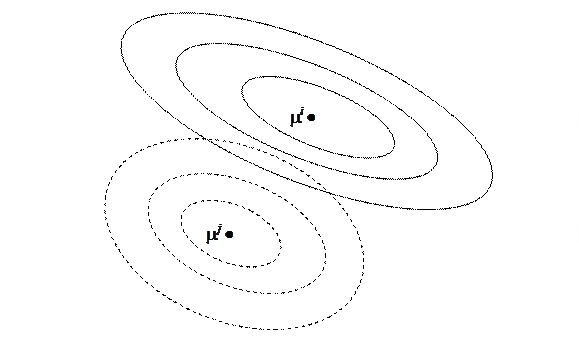
Рис. 9. Линии одинаковой плотности для двух классов
(нормальные распределения)

Таким образом, в двухмерном случае области граничат по прямым линиям. Можно доказать, что граничная гиперплоскость будет всегда перпендикулярной прямой, соединяющей центры распределений, т. е. точк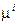и и 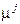в пространстве описаний. Точка, в которой гиперплоскость пересекает эту прямую, будет зависеть от относительной частоты каждого класса и цены ошибочной классификации.