Мультипликативные функции.

Введем функции 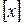– целая часть от x , 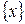– дробная часть от x.

Функция Θ(a) называется мультипликативной, если:

1. Определена для 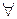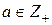, и при этом 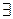a₁:Θ(a₁)≠0;

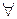
2. 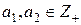: (a₁,a₂)=1 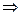Θ(a₁∙a₂)=Θ(a₁)∙Θ(a₂).

Пример:

Степенная функция 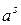– мультипликативная функция.

Свойства мультипликативных функций:

1. Если Θ(a) – мультипликативная функция, то Θ(1)=1.

Доказательство:

По определению мультипликативной функции, найдется a₁: Θ(a₁)≠0.

Тогда Θ(a₁)=Θ(a₁∙1)=Θ(a₁) ∙ Θ(1). Отсюда Θ(1)=1.

□

2. Если Θ – мультипликативная функция, то для попарно простых чисел a₁,a₂,…,a_k выполняется Θ(a₁∙a₂∙…∙a_k)= Θ(a₁)∙Θ(a₂)∙…∙Θ(a_k).

В частности,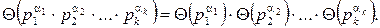

(Доказательство очевидным образом следует из 2-го условия на мультипликативную функцию.)

3. Если функции Θ₁, Θ₂, … ,Θ_k – мультипликативные, то их произведение Θ=Θ₁∙Θ₂∙…∙Θ_k – также мультипликативная функция.

4. Если Θ(a) – мультипликативная функция, 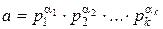– каноническое разложение а, то, обозначив знаком 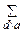сумму по всем делителям числа а, имеем

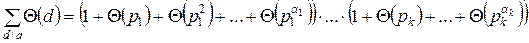
(Доказываем, раскрывая скобки в правой части).

Функция Эйлера.

Функция Эйлера φ(a) есть количество чисел ряда 0, 1, …, а–1, взаимно простых с а ( ).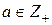

φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2, φ(5)=4, φ(6)=2 и т. д.

Свойства функции Эйлера:

1) φ(1)=1;

Доказательство следует из определения.

2) φ(p)=p–1, где р – простое;

Доказательство:

Действительно если р – простое, в ряду чисел 0, 1, …, p–1 не является взаимно простым с p только «0». Остальные p–1 чисел являются взаимно простыми с p в силу его простоты. Воспользовавшись определением функции Эйлера, получим искомое.

□

3)φ(p^α)=p^α–1(p–1) , где р – простое;

Доказательство:

Рассмотрим ряд чисел 0, 1, … , p, … , 2p, … , 3p, … , p², … ,(p+1)p, … ,p^α­--­­1­­­­.­

В этом ряду не взаимно простыми с p^α являются только те числа, которые кратны p, то есть числа 0, p, 2p, …, (p^α–1–1)p. Таких чисел будет p^α–1. Всего же чисел в этом ряду будет p^α.

Таким образом, количество чисел в рассматриваемом ряду, взаимно простых с p^α будет p^α–p^α–1= p^α–1(p–1). Итак, φ(p^α)=p^α–1(p–1).

□

4)φ(a) – мультипликативная функция.

Доказательство:

Действительно, по определению функции Эйлера, она задана для всех положительных чисел, и согласно свойству №1 функции Эйлера, φ(1)=1.

Покажем, что φ(p₁p₂)=φ(p₁)φ(p₂), если p₁, p₂ ­– простые числа.

Действительно, в ряду чисел 0, 1, … , p₁p₂—1 ровно p₂ чисел являются кратными p₁ и ровно p₁ чисел будут кратны p₂. Причем, в силу взаимной простоты p₁ и p₂, это будут разные числа, и только число «0» кратно и p₁, и p₂. Таким образом, чисел, кратных p₁ или p₂ будет p₁+p₂—1. Тогда чисел, взаимно простых и с p₁, и с p₂ будет ровно p₁p₂—p₁—p₂+1=p₁(p₂—1)—(p ₂—1) =(p₁—1)(p₂—1)= φ(p₁)φ(p₂).

Покажем теперь, что для взаимно простых чисел a₁ и a₂ справедливо φ(a₁a₂)=φ(a₁)φ(a₂).

Действительно, в ряду чисел 0, 1, … , a₁a₂—1 ровно a₁a₂—φ(a₁)a₂ чисел будут не взаимно простыми с a₁ и a₁a₂—φ(a₂)a₁ чисел – не взаимно простыми с a₂.

В то же время в ряду чисел 0, 1, … , a₁—1 ровно a₁— φ(a₁) чисел не будут являться взаимно простыми с a₁, в ряду чисел 0, 1, … , a₂—1 ровно a₂— φ(a₂) чисел не будут являться взаимно простыми с a₂. То есть среди чисел 0, 1, … , a₁a₂—1 не взаимно простыми одновременно и с a₁ , и с a₂ будут являться (a₁—φ(a₁))(a₂—φ(a₂)) чисел.

Таким образом, общее количество взаимно простых с a₁a₂ среди натуральных чисел, меньших a₁a₂, есть

a₁a₂—( a₁a₂—φ(a₁)a₂+ a₁a₂—φ(a₂)a₁—(a₁—φ(a₁))(a₂—φ(a₂)))=

= a₁a₂— (a₁a₂—φ(a₁)a₂— φ(a₂)a₁+ φ(a₁)a₂+ φ(a₂)a₁— φ(a₁)φ(a₂))= φ(a₁)φ(a₂).

Итак, доказали, что функция Эйлера – мультипликативная.



Пример

Вычислим φ(28350322).

Для того, чтобы вычислить значение функции Эйлера, необходимо найти каноническое разложение аргумента.

28350322=2·14175161=2·7·2025023=2·7²·289289=2·7³·41327=

=2·7³·11·3757=2·7³·11·13·289=2·7³·11·13·17².

φ(28350322)= φ(2·7³·11·13·17²)= φ(2) · φ(7³)· φ(11)· φ(13)· φ(17²)=

=1·7²·6·10·12·17·16=9596160.

Ответ: φ(28 350 322)=9 596 160.

Теория сравнений

Будем рассматривать целые числа в связи с остатками от деления их на данное целое положительное m – модуль. Если 2 целых числа a и b имеют одинаковый остаток от деления на m, то говорят, что они называются равноостаточными или сравнимыми по модулю m, и пишут a ≡ b (mod m), что равносильно a = b+mt, где t 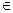Z, или m\(a–b) (очевидно)

3.1. Свойства сравнений:

1. a ≡ b (mod m), b ≡ c (mod m), 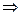a ≡ c (mod m)

2. a ≡ b (mod m) 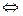b ≡ a (mod m)

3. a₁ ≡ b₁ (mod m), a₂ ≡ b₂ (mod m), … , a_k ≡ b_k (mod m) =>

a₁+…+a_k ≡ b₁+…b_k(mod m)

4. a+b ≡ c (mod m) 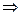a ≡ c–b (mod m)

5. a ≡ b (mod m) 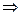a+mt ≡ b+mk(mod m) (t, k 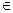Z)

6. a ≡ b (mod m), c ≡ d (mod m) 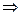ac ≡ bd (mod m)

7. a ≡ b (mod m) 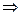a^k ≡ b^k(mod m)

8. a ≡ b (mod m) 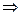ak ≡ bk(mod m)

9. Если a ≡ b (mod m), (a, b) = c, (c, m) = 1 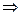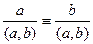(mod m)

10. a ≡ b (mod m) 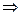ak ≡ bk (mod mk)

11. a ≡ b (mod m), a = a₁d, b = b₁d, m = m₁d 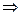a₁ ≡ b₁(mod m₁)

12. a ≡ b (mod m₁), a ≡ b(mod m₂), …, a ≡ b(mod m_k)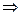

a ≡ b (mod НОК(m₁,…,m_k))

13. a ≡ b (mod m), d\m 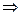a ≡ b(mod d)

14. d\a, d\m, a ≡ b(mod m) 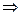d\b

15. a ≡ b (mod m) 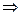(a, m) = (b, m)

Доказательство данных свойств не представляет сложности и может быть проведено читателем самостоятельно. Найти доказательства этих свойств можно в [5].