Полная система вычетов.

Совокупность чисел, сравнимых с a по модулю m называется классом чисел по модулю m (или классом эквивалентности). Все числа одного класса имеют вид mt + r при фиксированном r.

При заданном m, r может принимать значения от 0 до m—1, т.е. всего существует m классов чисел по модулю m, и любое целое число попадет в один из классов по модулю m. Таким образом,

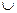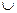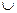Z = [0]_m [1]_m … [m—1]_m, где [r]_m={x 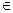Z: x≡r(mod m)}

Любое число класса [r]_m называется вычетом по модулю m по отношению ко всем числам того же класса. Число, равное остатку r, называется наименьшим неотрицательным вычетом.

Вычет, наименьший по абсолютной величине, называется абсолютно наименьшим вычетом.

Пример

Возьмем модуль m=5. И пусть a=8. Разделим a на m с остатком:

8=5·1+3.

Остаток r=3. Значит 8 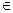[3]₅, и наименьший неотрицательный вычет числа 8 по модулю 5 есть 3.

Абсолютно наименьший вычет можно отыскать, вычислив r—m=3—5=—2, и сравнив абсолютные величины |—2| и |3|. |—2|<|3|, значит —2 – абсолютно наименьший вычет числа 8 по модулю 5.

Взяв от каждого класса по одному вычету, получим полную систему вычетов по модулю m. Если все эти числа будут являться наименьшими неотрицательными вычетами по модулю m, то такая система вычетов называется полной системой наименьших неотрицательных вычетов, и обозначается Z_m.

{0; 1;…; m—1} = Z_m – полная система наименьших неотрицательных вычетов.

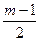{– ;…; 0;…; 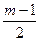} (если m–нечетное число) ;

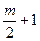{ — ,…,—1, 0, 1,…, 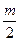} или {— 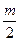,…, —1, 0, 1,…, 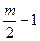} (если m четное число) – полная система абсолютно наименьших вычетов.

Пример

Если m=11, то полная система наименьших неотрицательных вычетов есть {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}, а полная система абсолютно наименьших вычетов – {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5}.

Утверждение 1

Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.

Доказательство:

Действительно, в силу несравнимости эти числа принадлежат к разным классам, а т.к. их m штук, то в каждый существующий класс попадает ровно одно число.



Утверждение 2

Если (a, m) = 1, и x пробегает полную систему вычетов по модулю m, то ax+b, где b – любое число из Z, тоже пробегает полную систему вычетов по модулю m.

Доказательство:

Чисел ax+b будет ровно m штук. Остается доказать, что любые 2 числа ax₁+b и ax₂+b несравнимы по модулю m, если x₁ 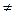x₂(mod m)

Доказательство от противного. Предположим, что ax₁+b ≡ ax₂+b (mod m) 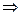в силу 4-го св-ва сравнений, ax₁ ≡ ax₂ (mod m) 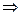в силу св-ва сравнений №9 и того, что (a, m) = 1, имеем x₁ ≡ x₂(mod m). Получили противоречие с тем, что x₁ 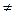x₂(mod m). Следовательно, предположение неверно, а значит верно обратное. То есть ax₁+b и ax₂+b несравнимы по модулю m, если x₁ 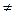x₂(mod m), что и требовалось доказать.