Единственность разложения на простые сомножители.

Утверждение 1.

Любое целое число a либо взаимно просто с данным простым р, либо р\а.

Доказательство:

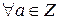, p – простое число, выполняется (a,p)\p. Тогда в силу простоты p, либо (a,p)=p, либо (a,p)=1. В первом случае р\а, во втором a взаимно просто с р. Что и требовалось доказать.

□

Теорема (Основное свойство простых чисел)

Если a₁,…,a_k 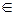Z, p\( a₁∙…∙a_k)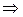 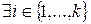: p\a_i.

Доказательство:

В силу утверждения 1, 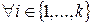либо (a_i,p)=1, либо (a_i,p)=p. Если бы 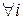выполнялось (a_i,p)=1 то выполнялось бы ( a₁∙…∙a_k, p)=1, и тогда p не делило бы (a₁∙…∙a_k). Получили противоречие с условием теоремы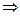 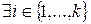: p\a_i.

□

Теорема (О единственности разложения на произведение простых чисел)

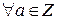, а>1 существует единственное разложение a=p₁∙p₂∙…∙p_n, где 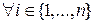, р_i – простое .

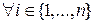Доказательство:

Действительно, обозначая буквой p₁ наименьший (простой) делитель а, имеем a=p₁a₁ Если a₁>0, то, обозначая p₂ наименьший (простой) делитель числа a₁, имеем a₁=p₂a₂ и т.д., пока не придем к a_n=1 для некоторого n (поскольку ряд a₁, a₂, …, a_n - убывающий ряд натуральных чисел, то рано или поздно мы придем к единице).

Тогда a=p₁∙p₂∙…∙p_n. Показали существование разложения на простые сомножители. Теперь докажем единственность.

Предположим, что для того же самого а существуетвторое разложение на простые сомножители a=q₁∙q₂∙…∙q_s, и, не нарушая общности, предположим, что s≥n. Тогда

p₁∙p₂∙…∙p_n = q₁∙q₂∙…∙q_s *

В силу основного свойства простых чисел, q₁\( p₁∙p₂∙…∙p_n) 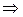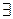i: q₁\p_i. Не нарушая общности, предположим, что i=1 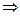q₁\p₁. В силу простоты чисел p₁, q₁, получим p₁=q₁. Сократив обе части равенства (*) на q₁, получим

p₂∙…∙p_n = q₂∙…∙q_s,

p₁=q₁

Повторив рассуждения для q₂, получим

p₃∙…∙p_n = q₃∙…∙q_s,

p₁=q₁, p₂=q₂

И т.д. В итоге получим

1=q_n+1∙…∙q_s,

p₁=q₁, p₂=q₂, … , p_n=q_n

Отсюда q_n+1=1, …, q_s=1. То есть оба разложения на простые сомножители тождественны.

□

В разложении числа на простые сомножители некоторые из сомножителей могут повторяться. Обозначая p₁,…, p_k различные из них, а α₁,…, α_k – кратности их вхождения в разложение, получим каноническое разложение числа а:

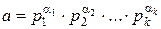
Добавим, что задача разложения числа на простые сомножители, или, иначе, задача факторизации, считается сложной задачей, поскольку известные алгоритмы факторизации имеют экспоненциальную или субэкспоненциальную сложность. Ознакомиться с такими алгоритмами можно будет в гл. 2 настоящего пособия.

Теорема (о делителях числа)

Пусть 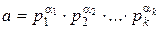– каноническое разложение числа a. Тогда все делители а имеют вид

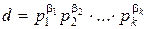, где 0≤β₁≤α₁, 0≤β₂≤α₂, …, 0≤β_k≤α_k.

Доказательство:

Пусть q\a a представимо в виде a=dq, тогда все простые делители числа d входят в каноническое разложение числа а с показателями, не меньшими тех, с которыми они входят в каноническое разложение числа а.

□

Следствие 1

Количество различных делителей числа 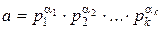есть .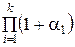

Доказательство очевидно, оно следует из числа всевозможных сочетаний в формуле делителя в теореме о делителях числа.

Следствие 2

НОД(a₁,…,a_n), где 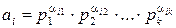( 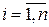), есть 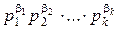, где ( ).

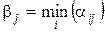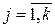Пример.

a₁=2∙3∙5²=150, a₂=2²∙5∙7=140, a₃=2³∙5=40.

p₁=2, p₂=3, p₃=5, p₄=7.

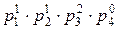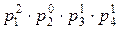a₁= , a₂= , a₃= .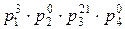

НОД(a₁,a₂,a₃)= 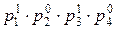=2∙5=10.

Следствие 3

Совокупность общих делителей a₁,…,a_n совпадает с совокупностью делителей НОД(a₁,…,a_n).

Следствие 4

НОК 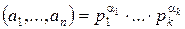, где ,

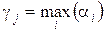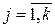
Пример.

НОК(150,140,40)=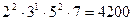

Следствие 5

Если a₁,…,a_n – попарно простые числа, то НОК(a₁,…,a_n)= a₁∙…∙a_n

Следствие 6

Совокупность общих кратных чисел a₁,…,a_n совпадает с совокупностью кратных их наименьшего общего кратного.

Доказательства следствий 1–6 предоставляется читателю в качестве упражнения. Отыскать эти доказательства можно в [5] (Виноградов, «Основы теории чисел»).