Наибольший общий делитель.
Теория делимости.
Открытие натуральных чисел было одним из величайших интеллектуальных достижений человечества. Что общего между тремя мамонтами, тремя звездами и тремя вздохами отвергнутого влюбленного? С точки зрения потребительских качеств ничего. Мамонт – это еда, вот она здесь у входа в пещеру, от нее зависит жизнь племени. Звезды в небе, их не потрогаешь, ночью их видно, а днем нет. Вздох вообще нечто не совсем материальное, отдельно от человека не существующее.
Очень не скоро было замечено, что общее между разными предметами и событиями то, что при их перечислении нужно загнуть одно и то же число пальцев на руке, в нашем примере три. Кстати, и до сих пор, (вспомните золотое детство), обучаясь счету, малыши загибают пальцы. С пальцами же связано и возникновение десятичной системы счисления. Кстати, если бы 400 млн. лет назад на берег из океана выползла не пятипалая двоякодышащая рыба, потомками которой мы являемся, а, например, с четырьмя лучами на плавнике, то победила бы восьмеричная система счисления.
Как бы то ни было, человечеством была освоена главная идея, лежащая в основе понятия о натуральном числе. Идея взаимно-однозначного соответствия или биекции между элементами разных множеств.
Множество натуральных чисел сейчас принято обозначать ажурной заглавной буквой N.Натуральными числами являются {1,2,3,…}. Понятие о нуле возникло гораздо позже, чем об остальных целых числах. Ноль обозначает ничто, однако 0 – вполне осязаемый символ ничем не хуже чем 1 или 5. Ноль – это нечто, а обозначает он ничто. Нечто обозначающее ничто – это уже шаг к раздвоению личности и он нормальным людям дался нелегко. Отрицательные числа (понимаемые как долг, как недостача) вошли в сознание людей гораздо проще, так же как и дроби, понимаемые как часть единого целого.
Основные понятия и теоремы.
Предмет теории чисел – целые числа и их свойства.
Множество целых чисел обозначается символом Z, символом Z+ обозначается множество целых положительных чисел, символом N– множество натуральных чисел. Латинскими малыми буквами здесь и далее будем обозначать целые числа.
Заметим, что 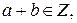
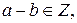

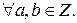
То есть как сумма, так и произведение целых чисел также являются целыми числами. Частное двух целых чисел не всегда является целым числом.
Если 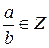 , (b≠0)
, (b≠0) 
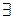
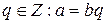 ,
,  Тогда говорят, что а делится на b, или b делит а, и пишут b\a. Тогда а называем кратным числа b, а b – делителем числа а.
Тогда говорят, что а делится на b, или b делит а, и пишут b\a. Тогда а называем кратным числа b, а b – делителем числа а.
Справедливы следующие
Теоремы:
(1) m\a, b\m  b\a.
b\a.
Доказательство:
m\a  a=ma1;
a=ma1;
b\m  m=bm1
m=bm1  a=bm1a1. Обозначив b1=a1m1, получим a=bb1, причем
a=bm1a1. Обозначив b1=a1m1, получим a=bb1, причем 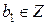
 b\a.
b\a.
□
(2) Если в равенстве вида k+l+…+n=p+q+…+s относительно всех членов кроме одного известно, что они кратны b, то и один оставшийся член тоже кратен b.
Доказательство:
Не нарушая общности, предположим, что таким членом (относительно кратности которого числу b ничего не известно) является k.
Тогда 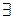 l1, …, n1, p1, q1, …, s1: l=bl1,…, n=bn1, p=bp1, q=bq1, …, s=bs1.
l1, …, n1, p1, q1, …, s1: l=bl1,…, n=bn1, p=bp1, q=bq1, …, s=bs1.
Тогда k=p+q+…+s–l–…–n=bp1+bq1+…+bs1–bl1–…–bn1=b(p1+q1+…+s1–l1–…–n1)
Обозначим k1= p1+q1+…+s1–l1–…–n1. Очевидно, k1 – целое число, причем k=bk1 Тогда, по определению делимости, b\k.
□
Кроме того, очевидны следующие свойства:
1) 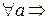 a\0, 1\a, a\a.
a\0, 1\a, a\a.
2) a\b, b\a  a=±b.
a=±b.
3) a\b, a\c 
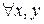 a\(bx+cy).
a\(bx+cy).
(Доказательство св-ва 3: b=ab1, c=ac1  bx+cy=ab1x+ac1y=a(b1x+c1y))
bx+cy=ab1x+ac1y=a(b1x+c1y))
Теорема деления (теорема о делении с остатком)

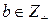
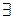 единственная пара чисел
единственная пара чисел 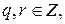 0 ≤ r < b: a=bq+r *
0 ≤ r < b: a=bq+r *
Доказательство:
Возьмем q: bq≤a, b(q+1)>a. Такое целое q, очевидно, существует  r=a–bq является целым положительным числом как разность двух целых чисел, первое из которых больше второго. Причем выполняется
r=a–bq является целым положительным числом как разность двух целых чисел, первое из которых больше второго. Причем выполняется 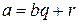 . Построением такого r доказано существование разложения (*).
. Построением такого r доказано существование разложения (*).
Теперь докажем единственность разложения (*): предположим, что кроме построенного выше, имеется еще одно разложение числа a:
a=bq1+r1, 0≤r1<b.
Вычтем полученное равенство из равенства (*) почленно. Получим
0=b(q–q1)+(r–r1). **
Поскольку b\0, b\b(q–q1), то по теореме 2, b\(r–r1).
С другой стороны, 0≤r<b, 0≤r1<b  |r–r1|<b. Отсюда и из того, что b\(r–r1), следует, что r–r1=0, и тогда r=r1. Подставляя полученное равенство в (**), получаем 0=b(q–q1).
|r–r1|<b. Отсюда и из того, что b\(r–r1), следует, что r–r1=0, и тогда r=r1. Подставляя полученное равенство в (**), получаем 0=b(q–q1).
Но по условию теоремы, b≠0 , тогда q–q1=0  q=q1.
q=q1.
Таким образом, оба построенных разложения числа a совпадают, а значит разложение (*) единственно.
□
В разложении (*) число q называются неполным частным, r – остатком от деления a на b.
Наибольший общий делитель.
Далее будем рассматривать лишь положительные делители чисел.
Общим делителем чисел a1, a2,…,an называется число d: d\ai 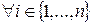 .
.
Наибольший из всех общих делителей чисел a1, a2,…,an называется их наибольшим общим делителем (НОД) и обозначается НОД(a1, a2,…,an) или (a1, a2,…,an).
Если (a1, a2,…,an)=1, то числа a1, a2,…,an называются взаимно простыми.
Если (ai,aj)=1 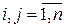 , i≠j , то числа a1, a2,…,an называются попарно простыми.
, i≠j , то числа a1, a2,…,an называются попарно простыми.
Утверждение
Если числа a1, a2,…,an – попарно простые, то они взаимно простые. (Очевидно.)
Теорема 1
Если b\a  совокупность общих делителей a и b совпадает с совокупностью делителей b. В частности, (a,b)=b.
совокупность общих делителей a и b совпадает с совокупностью делителей b. В частности, (a,b)=b.
Доказательство:
b\a  a=ba1, тогда
a=ba1, тогда 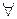 d: d\b справедливо d\a (т.е. любой делитель b является также делителем a).
d: d\b справедливо d\a (т.е. любой делитель b является также делителем a).
Если l\a, но l не делит b, то l не является общим делителем a и b.
То есть совокупность общих делителей a и b совпадает с совокупностью делителей b. А поскольку наибольший делитель b есть b, и b\a , то (a,b)=b.
□
Теорема 2
Если a=bq+c, то совокупность общих делителей a и b совпадает с совокупностью общих делителей b и c.
В частности, (a,b)=(b,c)
Доказательство:
Пусть m\a, m\b  m\c (в силу a=bq+c и теоремы 2 п.1), а значит m – общий делитель b и c.
m\c (в силу a=bq+c и теоремы 2 п.1), а значит m – общий делитель b и c.
Пусть l\b, l\c  l\a (в силу a=bq+c и теоремы 2 п.1), а значит l - общий делитель a и b.
l\a (в силу a=bq+c и теоремы 2 п.1), а значит l - общий делитель a и b.
Получили совпадение совокупности общих делителей a и b и общих делителей b и c.
Пусть теперь d=(a,b)  d\a, d\b, а значит, по доказанному выше, d\c. В силу совпадения совокупностей общих делителей и того, что d – наименьший изо всех делителей a и b, не может существовать d1: d1>d, d1\b, d1\c. Поэтому d=(b,c)
d\a, d\b, а значит, по доказанному выше, d\c. В силу совпадения совокупностей общих делителей и того, что d – наименьший изо всех делителей a и b, не может существовать d1: d1>d, d1\b, d1\c. Поэтому d=(b,c)  (a,b)= (b,c).
(a,b)= (b,c).
□
Алгоритм Евклида (отыскания НОД 2-х чисел)
Пусть a>b. Тогда в силу теоремы делимости находим ряд равенств:
a=bq1+r1, 0<r1<b
b=r1q2+r2, 0<r2<r1
r1=r2q3+r3, 0<r3<r2
...…………………
rn-2=rn-1qn+rn, 0<rn<rn-1
rn–1=rnqn+1.
Получение последнего равенства (то есть равенства с разложением без остатка) неизбежно, т.к. ряд b, r1, r2, …. – ряд убывающих целых чисел, который не может содержать более b положительных чисел, а значит рано или поздно в этом ряду возникнет «0».
Видим, что общие делители a и b, b и r1, r1 и r2,..., rn–1 и rn совпадают с делителями числа rn  (a,b)=(b,r1)=(r1,r2)=…=(rn-1,rn)= rn.
(a,b)=(b,r1)=(r1,r2)=…=(rn-1,rn)= rn.
Таким образом, (a,b)=rn.
Вышеизложенная идея нахождения НОД может быть реализована в виде алгоритма. Ниже приведены несколько вариантов реализации алгоритма Евклида.
Реализация алгоритма Евклида (вариант алгоритма с вычитанием)
Вход: a, b>0.
1.Если a>b  Шаг 3
Шаг 3
если a<b  Шаг 2
Шаг 2
если a=b  Шаг 5 (выход)
Шаг 5 (выход)
2.Меняем местами a и b.
3.a:=a–b
4.Возвращаемся на Шаг 1.
5. Выход: a – НОД
Ниже приведен пример использования этой реализации алгоритма.
Пример
a=603, b=108
Преобразования алгоритма записаны в таблицу, верхняя строка которой содержит значение переменной a, нижняя – содержимое переменной b. Каждый столбец таблице соответствует состоянию процесса на отдельном шаге.
| a | |||||||||||||||
| b |
Ответ: НОД(603,108)=9.
Реализация алгоритма Евклида (вариант алгоритма с делением с остатком)
Вход: a, b >0.
1. Находим разложение a=bq+r, 0≤r<b
2. если r=0  Шаг 5 (выход)
Шаг 5 (выход)
3. a:=b; b:=r.
4. Возвращаемся на Шаг 1
5. Выход: b – НОД.
Пример
a=603, b=108
| a | ||||||
| b |
603=5·108+63
108=1·63+45
63=1∙45+27
45=1∙27+18
27=1∙18+9
18=2∙9+0
Ответ: НОД(603,108)=9.
Бинарный алгоритм Евклида
Этот вариант создан специально для реализации на ЭВМ. В нем учитывается, что операция деления на число 2 или на любую степень двойки является весьма быстрой и простой операцией (в двоичной системе счисления операция деления на 2 есть всего лишь битовый сдвиг вправо).
Учтем, что (2k∙a,2s∙b)=2min(k,s)(a,b).
Алгоритм:
Вход: a, b>0.
1. Представим a и b в виде: 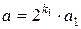 ;
; 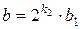 , где a1, b1 – нечетные числа.
, где a1, b1 – нечетные числа.
k:=min(k1,k2).
2. Если a1>b1  Шаг 4
Шаг 4
a1< b1  Шаг 3
Шаг 3
a1= b1  Шаг 6
Шаг 6
3. Меняем местами a1 и b1.
4. c:=a1–b1=2s∙c1 (c1 - нечетное число)
(Заметим, что с обязательно будет четным, а значит 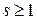 )
)
5. a1:= b1 , b1:=c1 . Возвращаемся на Шаг 1.
6. Выход: (a,b)=2k∙a1 .
Пример
a=603, b=108
| a1 | |||
| b1 | |||
| c1 | – |
1. a1=603, k1=0; b=108=4∙27=22∙27  k2=2, b1=27, k=0
k2=2, b1=27, k=0
2. a1=603> b1=27  Ш4
Ш4
4. c=603-27=56=64∙9, c1=9
5. a1=27; b1=9  Ш1
Ш1
1. a1=27; b1=9
2. a1> b1  Ш4
Ш4
4. c=a1–b1=18=2∙9, c1=9
5. a1=9, b1=9
1. a1=9, b1=9, k=0
2. a1= b1  Ш6
Ш6
6. (a,b) = 2º∙9=9
Для НОД справедливы следующие свойства:
1) (am,bm)=m(a,b) 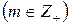
Доказательство:
Доказательство строится, умножая почленно соотношения алгоритма Евклида на m.
2) d – общий делитель чисел a и b 
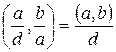
(в частности, 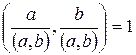 ).
).
Доказательство:
Учитывая, что 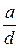 и
и 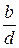 – целые числа, из свойства НОД №1 получаем соотношение
– целые числа, из свойства НОД №1 получаем соотношение 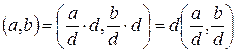

 , что и требовалось.
, что и требовалось.
□
3) (a,b)=1  (ac,b)=(c,b)
(ac,b)=(c,b)
Доказательство:
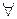 a, b, c выполняется (ac,b)\ac, (ac,b)\b
a, b, c выполняется (ac,b)\ac, (ac,b)\b  (ac,b)\bc
(ac,b)\bc  (ac,b)\(ac,bc).
(ac,b)\(ac,bc).
По условию теоремы, в силу взаимной простоты a и b  (ac,bc)=c, то есть получили (ac,b)\с.
(ac,bc)=c, то есть получили (ac,b)\с.
Но (ac,b)\b  (ac,b)\(c,b).
(ac,b)\(c,b).
С другой стороны, (c,b)\ac, (c,b)\b.  (c,b)\(ac,b).
(c,b)\(ac,b).
Таким образом, числа (ac,b) и (c,b). взаимно делят друг друга  (ac,b)=(c,b).
(ac,b)=(c,b).
□
4) (a,b)=1, b\ac  b\c.
b\c.
Доказательство:
Из теоремы №1 о НОД в силу b\ac,  (ac,b)=b.
(ac,b)=b.
из свойства НОД № 3  b=(c,b)и тогда из теоремы №1 о НОД b\c.
b=(c,b)и тогда из теоремы №1 о НОД b\c.
□
5) Если (ai, bj)=1 для 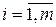 ,
, 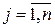
 (
( 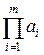 ,
, 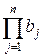 )=1.
)=1.
Доказательство:
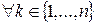 имеем (
имеем (  ,
, 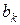 ) = (
) = ( 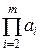 ,
, 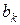 ) = (
) = (  ,
, 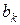 ) = … =
) = … = 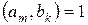 .
.
Аналогично, используя полученное соотношение,
( 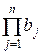 ,
,  ) = (
) = ( 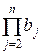 ,
,  ) = … = (
) = … = ( 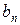 ,
,  ) = 1.
) = 1.
□
Дата добавления: 2015-11-28; просмотров: 2103;
