КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
Причинно-следственные отношения – связь явлений и процессов, когда изменение одного из них – причины – ведет к изменению другого - следствия. Социально-экономические явления – это результат одновременного воздействия большого числа причин.
Признак – основная отличительная черта, особенность изучаемого явления или процесса. Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, являются результативными. Мультиколлинеарность – наличие тесной связи между факторными признаками.
Функциональная связь – связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Стохастическая связь – связь, которая проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений.
Корреляционная связь – изменение среднего значения результативного признака, которое обусловливается изменением факторных признаков.
Прямая связь – с увеличением или уменьшением значения факторного признака увеличивается или уменьшается значение результативного.
Обратная связь – с увеличением или уменьшением значений факторного признака уменьшается или увеличивается значение результативного.
Линейная связь – статистическая связь между явлениями, выраженная уравнением прямой линии.
Нелинейная связь – статистическая связь между социально-экономическими явлениями, аналитически выраженная уравнением кривой линии (параболы, гиперболы и т.д.).
Корреляция – статистическая зависимость между случайными величинами, которая не имеет строго функционального характера, но изменение одной из случайных величин приводит к изменению математического ожидания другой. Корреляционный метод имеет своей задачей количественное определение тесноты связи между двумя признаками и между результативным и множеством факторных признаков.
В статистике различают следующие варианты зависимостей:
- Парная регрессия – аналитическое выражение связи двух признаков.
- Частная корреляция – зависимость между результативными и одним факторным признаками при фиксированном значении других факторных признаков.
- Множественная регрессия – модель связи трех и более признаков.
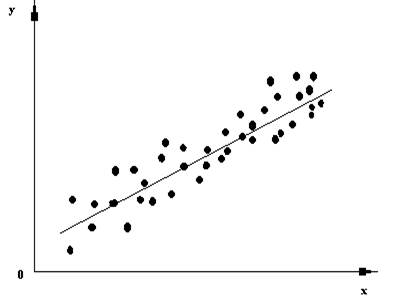
Рис. 3.1. Корреляционное поле
Регрессионный анализ – аналитическое выражение связи, в котором изменение одной величины – результативного признака – обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные или средние значения.
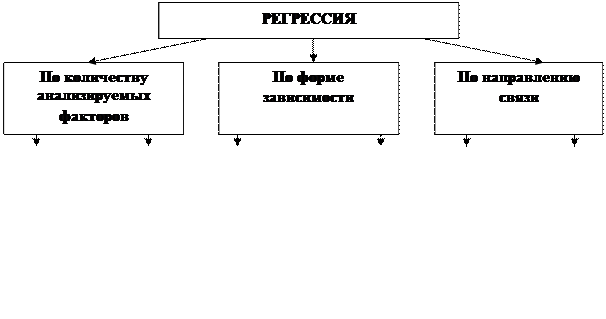
Рис. 3.2. Классификация типов регрессий
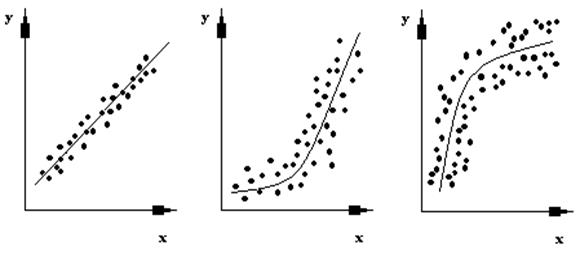
Рис. 3.3. Прямая (положительная) регрессия
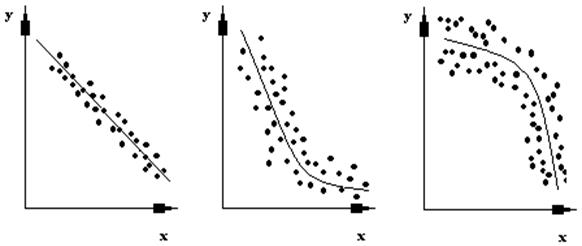
Рис. 3.4. Обратная (отрицательная) регрессия
 |
Рис. 3.5. Схема проведения корреляционно-регрессионного анализа
Таблица 3.1
| № п/п | Вид регрессии | Уравнение регрессии |
| 1. | линейная |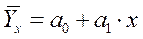 
|
| 2. | парабола второго порядка |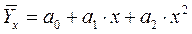 
|
| 3. | гипербола |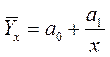 
|
В уравнении парной регрессии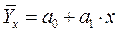 
коэффициент регрессии 
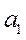отражает величину среднего абсолютного прироста результативного признака 
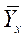при увеличении факторного признака на единицу.
Коэффициент регрессии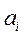 
показывает, на сколько в среднем изменяется значение результативного признака при изменении факторного на единицу собственного изменения.
Оценка параметров регрессии (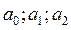 
) осуществляется методом наименьших квадратов (МНК) с использованием прикладных программ статистической обработки данных (SPSS, STATISTICA и др.).
Рис. 3.6. Схема построения уравнения парной регрессии
При построениямногофакторныхмоделей взаимосвязи используют пять типов моделей:
· линейную: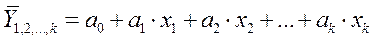 
· степенную: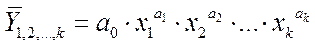 
· показательную: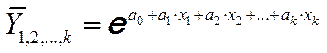 
· параболическую: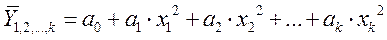 
· гиперболическую: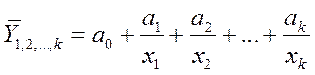 
Множественный коэффициент корреляции отражает связь между результативным и несколькими факторными признаками.Частный коэффициент корреляции показывает степень тесноты связи между двумя признаками при фиксированном значении остальных факторных признаков.
Проверка адекватности моделей, построенных на основе уравнения регрессии, начинается с проверки значимости каждого коэффициента регрессии с помощью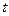 
-критерия Стьюдента: 
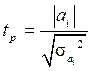, где 
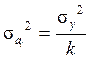- дисперсия коэффициента регрессии; 
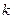- число факторных признаков; 
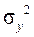- дисперсия результативного признака. Параметр модели признается статистически значимым, если 
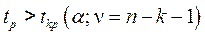, где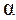 
- уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь, т.е. статистическая существенность связи утверждается при отклонении нулевой гипотезы об отсутствии связи; 
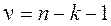- число степеней свободы, которое характеризует число свободно варьирующих элементов совокупности.
Проверка адекватности всей модели осуществляется с помощью расчета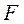 
-критерия и величины средней ошибки аппроксимации 
:
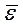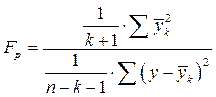и 
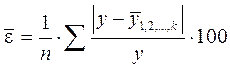, где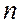 
- число наблюдений, 
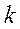- число факторных признаков в уравнении, 
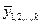- теоретические значения результативного признака, полученные по результатам регрессии. Если 
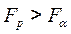при 
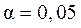или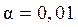 
, то гипотеза 
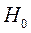- гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим отвергается; величина 
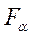определяется по специальным таблицам на основании величины 
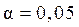или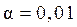 
и числа степеней свободы 
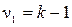и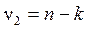 
. Значение средней ошибки аппроксимации не должно превышать 12-15%.
Рис. 3.7. Классификация пригодности регрессионной модели для принятия решений и осуществления прогнозов
Линейный коэффициент корреляции определяет тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
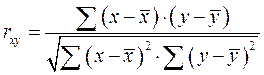
Таблица 3.2
Дата добавления: 2016-01-20; просмотров: 590;