Математичні моделі елементів електронних пристроїв

Математичні моделі елементів електронних пристроївзобража-ються в вигляді еквівалентних електричних схем. Прикладом таких моделей можуть бути еквівалентні електричні схеми моделі напівпровідникового діода та моделі Еберса-Мола біполярного транзистора.

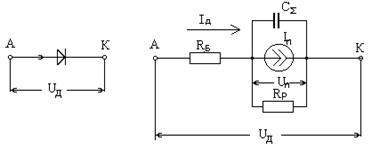
Модель діода, яка зображена на рис.5.1, є універсальною нелінійною моделлю, що описує електричні процеси в статичному та динамічному режимах в прямому і зворотному напрямках роботи, за винятком області пробою p-n переходу. Ця ММ придатна як для великих сигналів, так і для рисих в області низьких і середніх частот.

а) б)

Рисунок 5.1 – Графічне зображення а) та еквівалентна схема б) діода,

де Iд, Uд – струм і напруга діода; R_Б

І_П, Uп – струм і напруга через p-n перехід;

CS,– сумарна ємність (дифузійна та бар'єрна ємності) p-n переходу, що враховує накопичування зарядів в p-n переході;

Rр– опір розтікання p-n переходу;

R_Б– об’ємний опір бази діода;

До нинішнього часу розроблена велика кількість моделей біполярного транзистора. Найбільше розповсюдження одержала мо­дель Еберса-Мола.

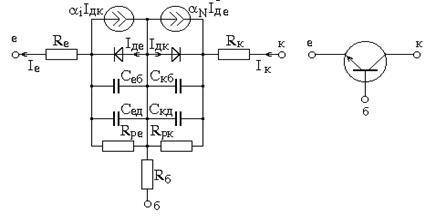
На рис. 5.2 зображену модель Еберса-Мола n-p-n транзистора,

де I_е , I_к – струми емітера та колектора;

I_дк , I_де – струми, інжектовані через переходи;

aN, a І– нормальний та інверсний коефіцієнти підсилення по струму в схемі із спільною базою;

U_е , U_к – напруга на емітерному та колекторному перехо­дах;

С_ед , C_еб, С_кд, C_кб – ємності дифузійні та бар'єрні емітерного та колекторного переходів;

R_б, R_к, R_е – об’ємні опори базової, колекторної та емітерної областей;

R_ре, R_рк – опори розтікання переходів.

а) б)

Рисунок 5.2 - Еквівалентна схема моделі Еберса-Мола для n- p-n транзистора (а) та його графічне зображення (б)

Більш детально математичні моделі цих та інших елементів електронних пристроїв описані в додатку А.

Макромоделі ІМС

Макромодель кола, або елемента кола - це система математичних cпіввідношень, що описує найбільш суттєві властивості кола, або елемента кола з певною точністю при заданих умовах.

Інтерес до макромоделі пов'язаний з розвитком інтегральної схемотехніки, що дозволило виготовляти ІМС, що містять 10² - 10⁵ і більше транзисторів на кристалі. Моделювати схеми з такою кількістю компонентів на рівні моделей транзисторів безглуздо. Необхідно понизити рівень складності таких схем. Одним з найбільш раціональних підходів для розв'язання цієї задачі є макромоделювання. Цей підхід дозволяє скоротити час моделювання в декілька десятків разів при зменшенні точності всього лише на 5 - 10%, що у більшості випадків цілком допустимо.

Типовий процес розробки макромоделі нагадує типовий процес розробки електронної схеми і складається з наступних етапів:

– розробка ТЗ, в якому вказуються перелік і точність параметрів та характеристик ІМС, що відображаються, діапазони їхніх змін, умови навколишнього середовища, дестабілізуючі фактори та ступінь їх врахування, вимоги, що витікають з особливостей формування та розв'язання рівнянь схеми в конкретній програмі АСхП, і т. п. Обов'язковим пунктом ТЗ є програма тестування та умови прийомки макромоделі;

– аналіз технічних матеріалів, даних ТУ, вимірів та інших даних на ІМС та розробка (синтез) на їхній основі структури та еквівалентної схеми макромоделі і нелінійних функцій, що підлягають програмуванню;

– визначення системи параметрів макромоделі, методик їх розрахунку;

– програмування необхідних нелінійних функцій та введення їх в бібліотеку нелінійних функцій програми АСхП;

– тестування макромоделей (моделювання контрольних задач та схем виміру параметрів ІМС) та доопрацювання макромоделі (корегування значень параметрів або еквівалентної схеми) до вимог ТЗ;

– випуск необхідної документації на макромодель;

– включення макромоделі до бібліотеки моделей і параметрів програми АСхП.

Як правило, макромодель ІМС розробляється гібридним або формальним способами, при яких основна увага звертається на відображення вихідних параметрів ІМС. Тільки деякі макромоделі відносно нескладних ІМС розробляються з допомогою фізичного методу, використовуючи в якості початкового варіанту її повну принципову електричну схему. Вона розбивається на функціональні блоки, що після цього спрощуються, а для макромоделі залишають їх найбільш істотні елементи та функції. Такі макромоделі, як правило, більш інформативні, ніж формальні.

Можна виділити типову структуру макромоделі схемотехніч-ного рівня (рис.5.3). Типові блоки I та III макромоделі здійснюють необхідне сполучення її внутрішніх змінних із змінними зовнішніх кіл. Вони відображають опори та інерційні властивості вхідних та вихідних кіл.

I II III

Рисунок 5.3 - Типова структура макромоделі схемотехнічного рівня

Перетворювальний блок II не пов'язаний з зовнішніми колами, а з блоками II і III пов'язаний тільки по управлінню. Тут відбувається перетворення вхідних сигналів в вихідні. Інколи тут враховується і сумарна інерційність внутрішніх кіл ІМС.

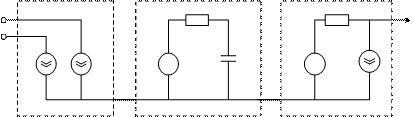
Макромоделі логічних ІМС. Особливо чітко виділяється описана вище структура у макромоделей логічних ІМС. Типовим прикладом таких макромоделей може бути макромодель двовходового ТТЛ-вентиля І-НІ (рис. 5.4).

Тут джерела струму J1 і J2 відображають вхід 1 і вхід 2 та задаються у вигляді таблиць або діодами. Джерело напруги

E1=f (I1, I2) реалізує логічну функцію вентиля, а його інерційні властивості - елементи R1, C1. Кероване джерело E2=f (UC1) відображає вихідну напругу вентиля, а опір R2 - вихідний опір. Генератор струму J₀ введений для часткового врахування зміни режимів вихідного кола.

+ U_ЖИВ

U1

U2

U_ВИХ

а)

I II III

U1 R1 R2

U2 + +

J2 J1 E1 C1 E2 J0 - - -

б)

Рисунок 5.4 – Двовходовий ТТЛ-вентиль: принципова електрична схема (а), макромодель (б).

При розробці макромоделей логічних ІМС враховується, що електричні характеристики по зовнішнім виводам ІМС в межах серії

або навіть декількох серій ідентичні, так само як ІМС, які виконують різноманітні логічні операції, мають однакові побудови вхідних і вихідних кіл. Так, для всіх ТТЛ ІМС входами є емітери багатоемітерних транзисторів, а виходами - складні інвертори. Тому вхідне коло в макромоделях ТТЛ та ТТЛШ схем задається спрощеною моделлю багатоемітерного транзистора. Для КМОП схем модель вхідного кола складається з вхідних опорів та ємностей.

Ця особливість логічних ІМС врахована в програмі МАЕС-П при побудові універсальної моделі логічних ІМС.

Макромоделі аналогових ІМС. Макромоделі аналогових схем будуються, як правило, поблочно, що відповідає структурі самих схем. Сучасні аналогові ІМС відрізняються регулярністю структури. Це дозволяє виділити як типові наступні каскади: диференціальний підсилювач, відзеркалювач струму, вихідний підсилювач, проміжний підсилювальний каскад по схемі із спільним емітером. Для типових каскадів розробляються відповідні моделі з врахуванням режимів їхньої роботи. Моделі типових каскадів спільно з рядом джерел, що керуються, утворюють базовий набір макроелементів, що використовуються для оперативного створення макромоделей аналогових та цифро-аналогових приладів.

Але при складанні макромоделей аналогових схем часто застосовують евристичні прийоми. Спочатку розглядається ідеальна макромодель, що відображає основну функцію, що виконується аналоговим пристроєм, а після цього починають поступове підвищен-ня точності введенням до складу ідеальної макромоделі додаткових елементів, що характеризують відхилення або нестабільність виконання цієї функції.

Розглянемо цю методику на прикладі макромоделі операційного підсилювача (ОП).

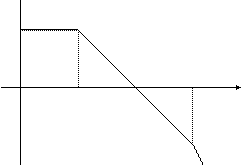
Коефіцієнт підсилення ОП. Коефіцієнт підсилення ОП залежить від частоти. Типовий графік Боде для амплітудного відгуку показаний на рис. 5.5. Кожна точка перегину на характеристиці відповідає від'ємному дійсному полюсу і може бути змодельована електричним колом, показаним на рис. 5.6, з коефіцієнтом передачі виду

, .

.

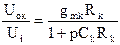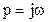20log A_iо

ω2 ω

ω1 логарифм

масштаб

Рисунок 5.5 – Графік Боде для ОП

Коефіцієнт підсилення цієї к-тої ланки за постійним струмом рівний gmкRк, а його полюс розміщений в точці - 1/RкCк. Подібні ланки зв'язані одна з одною через джерела струму, що керуються напругою, що забезпечує їхню розв'язку. Число ланок залежить від того, скільки полюсів необхідно відобразити в моделі. Коефіцієнт підсилення A_iо = Uo/Uiрозподіляється по всім ланкам.

+ +

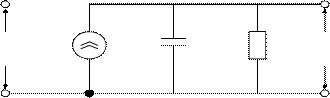U_iK g_mkU_iK C_K R_K U_0K

_ _

Рисунок 5.6 – Ланка, що моделюєк-й полюс

Обмеження швидкості зростання. Швидкість зростання вихідної напруги Sr - це максимальна швидкість зміни вихідної напруги, що досягається в ОП. Sr є важливим параметром для кіл, що підсилюють сигнали, які швидко змінюються. Швидкість зростання моделюється ланкою, показаною на рис. 5. 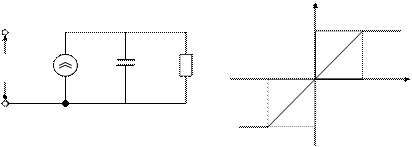7 I

I_m

С R

U_ik J=f(U_jk) - Û_ik U

+Û_ik

-I_m

Рисунок 5.7 – Нелінійна провідність, що моделює обмеження швидкості зростання напруги

Вона містить нелінійне джерело струму, що керується напругою, завдяки чому максимальний струм через конденсатор не перевищує Im. Тому швидкість зміни напруги на конденсаторі обмежена:

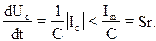
Резистор, зображений на рис. 5.7, забезпечує шлях для розряду конденсатора. Порівнюючи рис. 5.7 і рис. 5.6, помічаємо, що ланка,

що обмежує швидкість зростання, вводить до моделі ОП полюс. У цьому випадку величина Û_iK на рис. 5.7 вибирається з рівняння

Û_iK = Im/ gmk .

Обмеження вихідої напруги. Якщо коефіцієнт підсилення ОП

A_iо = gm1R1 *Ошибка! Источник ссылки не найден. gm2R2 *…*Ошибка! Источник ссылки не найден. gm0Ro

розмістити в першому RC колі, а у всіх інших зробити Кu = 1 (тобто gm1R1= A_iо, gm2R2= ... = gm0 Ro= 1), то тоді можна обмежити вихідну напругу ОП Uo до Uomax в цьому ж колі, якщо вольт-амперну характеристику резистора R1 зобразити у вигляді джерела напруги Е1 (рис. 5.8). Це безумовно підвищить збіжність обчислювального процесу, тому що ліквідується перенапруга на R1.

UE1

U0max

U0max

R1

U0max IE1

R1

U0max

Рисунок 5.8 – Вольт-амперна характеристика резистора

Макромодель ОП з двома полюсами, що враховує викладені вище характеристики, зображена на рис. 5.9, де вхідне коло моделює опори R+, R -, Ri, а вихідне - опір Ro.

Приклад.

Побудувати макромодель ОП з наступними параметрами (відповідно до ТУ):

- коефіцієнт підсилення без зворотного зв'язку A_iо =2* 105;

- вхідні опори: Ri=2 мОм, R+=R-=2000 мОм;

- вихідний опір Rо=75 Ом;

- пікове значення вихідної напруги Uомах=10В;

- максимальна швидкість зростання напруги Sr=0, 5 В/мкс;

- частота домінуючого полюсу w 1= 10*p рад/сек;

- частота другого полюсу w 2=4 p *10⁶ рад/сек.

Макромодель ОП зображена на рис. 5.9.

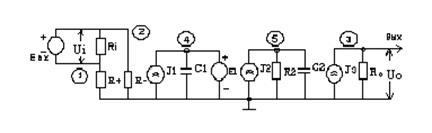
Рисунок 5.9 – Макромодель ОП з двома полюсами

В макромоделі існують опори Ri, R+, R -, Rо, яким задаємо їхні відповідні значення.

Виберемо (довільно) R1=100 кОм, R2=100 Ом.

Значення w1 і w2дають можливість визначити ємності С1 і С2:

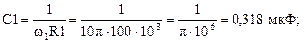
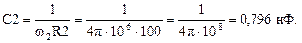
Умова підсилення за постійним струмом виконується, якщо

A_iо = gm1R1 *Ошибка! Источник ссылки не найден. gm2R2 *Ошибка! Источник ссылки не найден. gm0Ro = 2 *105,

gm1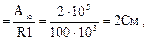

де gm1– крутість функції f1 в лінійній області.

gm2R2=1, gm2=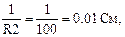

gm0Ro=1, gm0=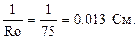

Залишилося визначити тільки нелінійності.

Нелінійний опір R1, що обмежує вихідну напругу Uo до рівня Uомах=10 В, зображуєм в вигляді нелінійного джерела напруги

UE1=f2(IE1) ( див.рис. 5.8).

Значення відповідного струму через R1 при UE1= Uомах=10 В

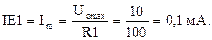
Умова обмеження швидкості зростання вимагає, щоб:

IC1= I_m= C1*Sr=0,318мкФ*0.5В/мкc=159 мА

та U1=I_m/g_m1=159мА/2См=79,5мВ.

Нелінійні залежності IJ1=f1(UR1), UE1=f2(IE1) наведені на

рис. 5.10 .

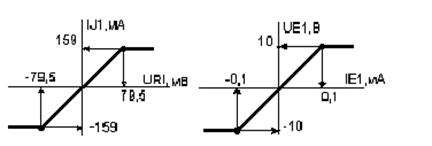
Рисунок 5.10 – Нелінійні залежності IJ1=f1(UR1), UE1=f2(IE1).