Формування рівнянь електричної схеми
В залежності від вибраного координатного базису (змінних незалежних рівнянь) виділяють наступні методи формування математичної моделі схеми (ММС) :
- контурних струмів,
- змінних стану,
- вузлових потенціалів.
Координатний базис утворюють змінні лінійно-незалежних рівнянь ММС, тобто рівнянь, які неможливо отримати перетворенням інших рівнянь ММС.
Для метода контурних струмів базисними змінними є контурні струми, або струми хорд. Гілки, які не ввійшли до дерева, називаються хордами. Цей метод використовують в основному, коли в схемі багато індуктивностей і взаємоіндуктивностей. Метод практично не використовується в програмах АСхП.
Змінними стану є струми в індуктивностях і напруги на ємностях, або в більш загальному випадку заряди на ємностях і потокозчеплення в індуктивностях. Через ці змінні можливо ви-разити усі інші струми та напруги в схемі. В цьому базисі фор-муються диференціальні рівняння в формі Коші, тобто вирішені відносно першої похідної
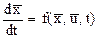 ,
, 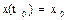 при t=t0=0;
при t=t0=0;
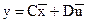 ,
,
де 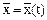 - змінні стану;
- змінні стану; 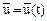 - вхідні сигнали;
- вхідні сигнали;
 - вихідні змінні; С,D- матриці коефіцієнтів.
- вихідні змінні; С,D- матриці коефіцієнтів.
Метод змінних стану був розповсюджений в 60-80 роках, коли застосовувались в основному класичні явні методи інтегрування. Але ці методи виявились безсилими для розв’язання ММС більшості електронних пристроїв, які мають великі розкиди сталих часу.
На їх зміну прийшли неявні методи інтегрування, які не такі критичні до цих розкидів, як явні, і не потребують формування ММС в формі Коші. Крім того, для формування ММС в базисі змінних стану використовується досить складна процедура, яка заснована на виборі і використанні дерева графа - сукупності гілок , які з’єднують всі вузли схеми, але не створюють контурів. Така процедура виявилась не зручною для видів моделювання, що вимагають частої варіації параметрів, наприклад, статистичного аналізу, оптимізації та інших.
Тому в кінці 80-х років від цього методу відмовились і практично у всіх програмах АСхП почали використовувати метод вузлових потенціалів, який дозволив значно спростити процедуру формування ММС та використати неявні методи чисельного інтегрування. Як базисні зміни тут використовуються потенціали вузлів.
В сучасних програмах АСхП формування рівнянь, як правило, здійснюється на основі методу вузлових потенціалів. Цей метод ми і будемо розглядати.
Формування за допомогою методу вузлових потенціалів базується на I законі Кирхгофа: сума струмів будь-якого вузла дорівнює нулю.
Розглянемо коло (рис. 5.11)
.
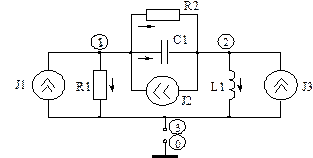
Рисунок 5.11- Електронне коло з трьома джерелами струму
Запишемо I закон Кирхгофа для вузлів 1-3, де представимо реактивні опори в операторній формі 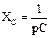 , XL= pL ;
, XL= pL ;
В матричному виді ці рівняння записуються так:
      G1+G2+pC1 – G2 – pC1 -G1 U1 J1+J2
-G2 – pC1 G1+G2+pC1 – G2 – pC1 -G1 U1 J1+J2
-G2 – pC1 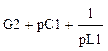  * U2 = J3-J2 .
-G1 * U2 = J3-J2 .
-G1 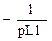 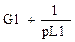 U3 -J1-J3 U3 -J1-J3
|
Або в компактній формі Y*U = J,
де Y- матриця провідності, а U, J - вектори вузлових потенціалів та незалежних джерел струмів.
 Проаналізувавши одержану матрицю провідностей, сформулюємо правила складання рівнянь електронного кола для вузлових потенціалів.
Проаналізувавши одержану матрицю провідностей, сформулюємо правила складання рівнянь електронного кола для вузлових потенціалів.
1. Діагональні елементи yii матриці Y позитивні і дорівнюють сумі провідностей, підключених до вузла i.
2. Позадіагональні елементи yjk матриці Y від'ємні і дорівнюють сумі провідностей між j та k - вузлами.
3. Довільний елемент вектору J jj дорівнює сумі струмів незалежних джерел, втікаючих в j-й вузол зі знаком плюс та витікаючих з нього зі знаком мінус.
Слід відзначити, що якщо один з вузлів заземлений, то з матриці зникають відповідний стовпець та відповідний рядок.
Сформульовані правила корисні при складанні рівнянь людиною. Вони дозволяють записати рівняння при послідовному переборі всіх вузлів. При складанні рівнянь за допомогою ПК більш прийнятним є підхід, заснований на послідовному переборі елементів схеми (дивись додаток Б).
Дата добавления: 2015-11-28; просмотров: 1005;
