Классическое определение вероятности. События называются равновозможными, если при данном испытании каждое из них имеет одинаковую возможность наступить
События называются равновозможными, если при данном испытании каждое из них имеет одинаковую возможность наступить. Элементарными событиями называются равновозможные и единственно возможные события, которые могут наступить при данном испытании.
Пример 10. Бросается игральный кубик. Обозначим события:
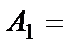 {выпало одно очко};
{выпало одно очко};
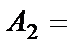 {выпало два очка};
{выпало два очка};
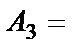 {выпало три очка};
{выпало три очка};
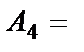 {выпало четыре очка};
{выпало четыре очка};
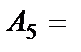 {выпало пять очков};
{выпало пять очков};
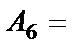 {выпало шесть очков};
{выпало шесть очков};
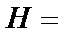 {выпало нечётное число очков}.
{выпало нечётное число очков}.
События 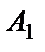 ,
, 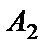 ,
,  ,
, 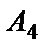 ,
, 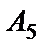 и
и 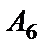 являются равновозможными и единственно возможными, т.е. элементарными. Наступление каждого из событий
являются равновозможными и единственно возможными, т.е. элементарными. Наступление каждого из событий 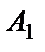 ,
, 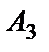 и
и 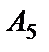 приводит к наступлению события Н. Эти события называются благоприятствующими для события Н.
приводит к наступлению события Н. Эти события называются благоприятствующими для события Н.
Пусть в результате испытания может наступить конечное число n элементарных событий. Среди этих событий имеется k таких, наступление которых ведёт к наступлению некоторого события А.
Вероятностью события А называется отношение числа k элементарных событий, благоприятствующих для события А, к числу n всех возможных элементарных событий: 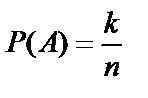 .
.
Такое определение вероятности называется классическим.
Пример 11. Брошен игральный кубик. Найти вероятность того, что число выпавших очков будет нечётным.
Решение. Обозначим события:
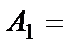 {выпало одно очко};
{выпало одно очко};
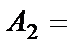 {выпало два очка};
{выпало два очка};
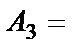 {выпало три очка};
{выпало три очка};
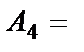 {выпало четыре очка};
{выпало четыре очка};
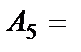 {выпало пять очков};
{выпало пять очков};
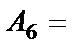 {выпало шесть очков};
{выпало шесть очков};
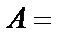 {выпало нечётное число очков}.
{выпало нечётное число очков}.
Всех возможных элементарных событий шесть, т.е. n=6. Благоприятствующими для А будут события 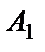 ,
, 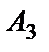 и
и 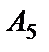 , т.е. k=3. Таким образом,
, т.е. k=3. Таким образом, 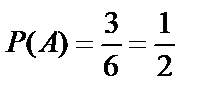 .
.
Из классического определения вероятности следуют её свойства:
 Вероятность достоверного события равна единице:
Вероятность достоверного события равна единице: 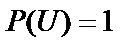 .
.
 Вероятность невозможного события равна нулю:
Вероятность невозможного события равна нулю: 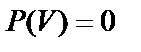 .
.
 Вероятность случайного события А находится в интервале (0,1):
Вероятность случайного события А находится в интервале (0,1): 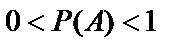 .
.
Таким образом, вероятность любого события находится в промежутке [0,1].
Дата добавления: 2016-01-16; просмотров: 1124;
