Случайные события и их классификация

Теория вероятностей – это раздел математики, изучающий закономерности массовых однородных случайных явлений.

Основными исходными понятиями в теории вероятностей являются понятия испытания (опыта) и события. Всякое действие, результат которого фиксируется, называется испытанием (опытом), а результат испытания или испытаний называется событием. Будем говорить, что в результате испытания или испытаний происходит (наступает) событие.

Пример 1. Подбросим над столом монету. При этом возможны два результата: монета упадёт на стол и на верхней её грани будет «герб» или же на верхней грани монеты будет «цифра». В этом случае будем говорить: выпал «герб» или выпала «цифра». В данном примере подбрасывание монеты является испытанием, а выпадение «герба» или выпадение «цифры» являются событиями, т.е. в результате подбрасывания монеты может произойти одно из двух рассмотренных событий.

Пример 2. Подбросим монету два раза подряд. При этом возможны следующие события: {оба раза выпал «герб»}, {оба раза выпала «цифра»}, {первый раз выпал «герб», а второй раз – «цифра»}, {первый раз выпала «цифра», а второй раз – «герб»}.

Все рассматриваемые события можно подразделить на достоверные, невозможные и случайные.

Событие называется достоверным, если при данном испытании оно обязательно произойдёт. Событие называется невозможным, если при данном испытании оно не может произойти. Случайным называется событие, которое при данном испытании может произойти или не произойти.

Пример 3. В урне находятся только красные шары. Проведём испытание – извлечём из урны один шар. Событие {извлечён красный шар} является достоверным, так как в урне только красные шары. Событие {извлечён белый шар} является невозможным, так как в урне нет белых шаров.

Пример 4. Стрелок произвёл один выстрел по мишени. При этом может произойти одно из двух событий: {есть попадание в мишень} или {нет попадания в мишень}. Оба эти события случайные.

Случайные события принято обозначать заглавными буквами латинского алфавита A, B, C, …; достоверные события – буквой U и невозможные – буквой V.

Случайные события подразделяются на совместные, несовместные и единственно возможные.

События называются совместными, если при одном и том же испытании наступление одного из них не исключает наступление других, т.е. они могут произойти совместно.

События называются несовместными, если при одном и том же испытании наступление одного из них исключает наступление других, т.е. они не могут произойти совместно.

Пример 5. По цели стреляют два стрелка. Обозначим события:

А = {первый стрелок попал в цель};

В = {второй стрелок попал в цель}.

События А и В будут совместными, так как попадание одного из стрелков в цель не исключает попадание другого.

Пример 6. Подбрасывается монета. В результате могут произойти события:

А = {выпал «герб»};

В = {выпала «цифра»}.

События А и В несовместны, так как наступление одного из них исключает наступление другого.

События называются единственно возможными, если при данном испытании произойдёт хотя бы одно из них. Два единственно возможные и несовместные события называются противоположными. Если А – некоторое событие, то ему противоположное обозначается 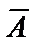. Совокупность единственно возможных и несовместных событий образует полную группу событий.

Пример 7. В урне находятся белые, чёрные и красные шары. Из урны извлекается один шар. Обозначим события:

А = {извлечён белый шар};

В = {извлечён чёрный шар};

С = {извлечён красный шар}.

События А, В, С являются единственно возможными.

Пример 8. Стрелок выстрелил по цели. Обозначим события:

А = {есть попадание в цель};

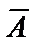= {нет попадания в цель}.

Эти события являются противоположными.

Пример 9. Бросается игральный кубик, на гранях которого написаны цифры 1, 2, 3, 4, 5 и 6. Эти цифры обозначают число очков. При бросании кубика на верхней его грани выпадет одна из этих цифр. Обозначим события:

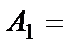{выпало одно очко};

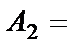{выпало два очка};

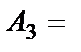{выпало три очка};

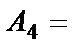{выпало четыре очка};

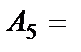{выпало пять очков};

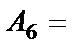{выпало шесть очков}.

Эти события являются единственно возможными и несовместными. Следовательно, они образуют полную группу событий.