Элементы комбинаторики. При непосредственном вычислении вероятности события А часто рассматриваются различные комбинации из множества n элементов по m элементов .
При непосредственном вычислении вероятности события А часто рассматриваются различные комбинации из множества n элементов по m элементов 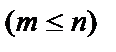 .
.
Перестановками из n элементов называются всевозможные упорядоченные множества, содержащие все данные n элементов. Число всех перестановок обозначают 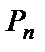 и находят по формуле
и находят по формуле
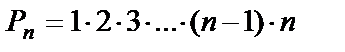 или
или 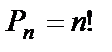 (n факториал).
(n факториал).
По определению принимают 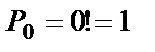 .
.
Пример 12. Какие трёхзначные числа можно образовать из неповторяющихся цифр 1, 2, 3.
Решение. 123, 132, 213, 231, 312, 321. Эти числа называются перестановками и их шесть.
Пример 13. Сколько существует способов, чтобы расположить в один ряд на полке 6 книг?
Решение. Число перестановок равно 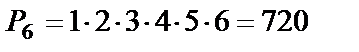 .
.
Размещениями из n элементов по m элементов (m<n) называются всевозможные упорядоченные множества по m элементов, образованные из данных n элементов и отличающиеся друг от друга или самими элементами, или их порядком. Обозначается число размещений из n элементов по m элементов символом 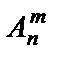 и вычисляется по формуле
и вычисляется по формуле 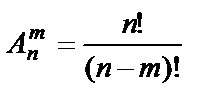 .
.
Пример 14. Какие двузначные числа можно образовать из цифр 1, 2, 3, если каждая цифра входит в число только один раз?
Решение. 12, 21, 13, 31, 23, 32. Таких цифр шесть.
Пример 15. Студенты данного курса изучают 7 учебных предметов. В расписание занятий можно поставить 3 различных предмета в день. Сколько существует способов, чтобы составить расписание на один день?
Решение. Количество способов равно числу размещений из 7 элементов по 3 элемента: 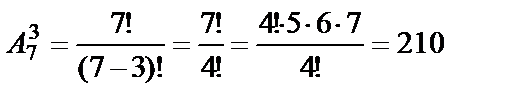 .
.
Сочетаниями из n элементов по m элементов называются всевозможные множества по m элементов, образованные из данных n элементов и отличающиеся друг от друга хотя бы одним элементом.
Обозначается число сочетаний из n элементов по m элементов символом 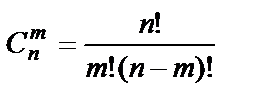 .
.
Пример 16. В урне находятся 3 белых шара и 7 чёрных. Из урны наугад извлекают два шара. Сколько существует способов, чтобы извлечь: а) два белых шара; б) два чёрных шара; в) один белый шар и один чёрный?
Решение. а) Так как в урне белых шаров только 3, то количество способов извлечь 2 белых шара равно числу сочетаний из 3 элементов по 2 элемента: 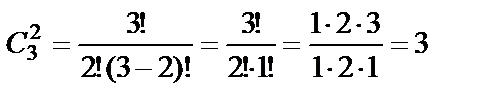 .
.
б) Чёрных шаров в урне 7, поэтому количество способов извлечь 2 чёрных шара равно 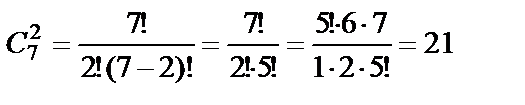 .
.
в) Количество способов извлечь один белый шар и один чёрный равно 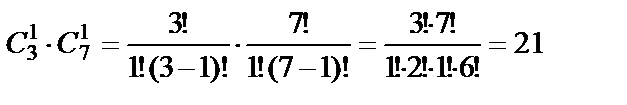 .
.
Пример 17. В ящике находятся 20 деталей первого сорта и 10 деталей второго сорта. Из ящика наугад берут 5 деталей. Найти вероятность того, что среди них окажутся 3 детали первого сорта и 2 - второго.
Решение. Обозначим событие A={взятыми окажутся 3 детали первого сорта и 2 - второго}. Искомая вероятность равна 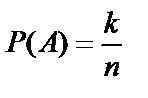 , где k – количество способов взять 3 детали первого сорта и 2 – второго, n – количество способов взять 5 деталей из 30. Тогда
, где k – количество способов взять 3 детали первого сорта и 2 – второго, n – количество способов взять 5 деталей из 30. Тогда 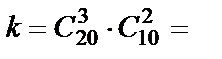
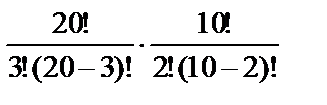
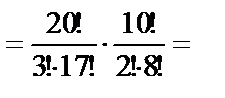
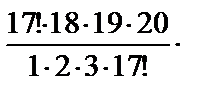
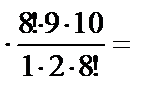
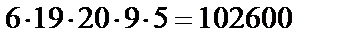 ;
; 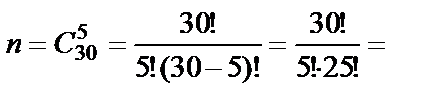
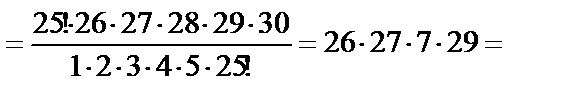 134386;
134386; 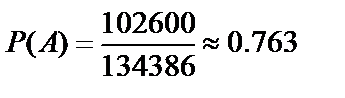 .
.
Дата добавления: 2016-01-16; просмотров: 1032;
