Пересечение прямой линии с плоскостью общего положения

Построение точки пересечения прямой с плоскостью общего положения выполняется по следующему алгоритму:

1) через данную прямую (MN) провести некоторую вспомогательную плоскость (g);

2} построить прямую (ED), линию пересечения данной плоскости (АВС) и вспомогательной плоскости (g);

3) определить положение точки (К) пересечения данной прямой (MN) и построенной линии пересечения (ED);

4) определить видимость прямой (MN) относительно плоскостей Н и V.

На рис.3.43 прямая MN пересекает плоскость, заданную треуголькомАВС. Через прямую MN проводим

ником АВС. Через прямую MN проводим

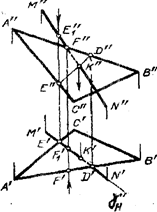горизонтально проецирующую плоскость g. Так как вспомогательная плоскость g горизонтально - проецирующая, то и горизонтальной проекцией плоскости g и треугольника АВС является прямая линия E'D'. Находим ее фронтальную проекцию E'D". Затем построим К",в которой E"D" пересекает M"N" и определяем ее горизонтальную проекцию К'. Определяем видимость отрезков МК и

Рис.3.44 Рис.3.45 3.46

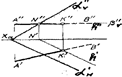
На рис.3.44 прямая АВ пересекает плоскость а общего положения. Проводим через прямую АВ горизонтально - проецирующую плоскость b, находим линию пересечения плоскости а и плоскости b (MN).

Определяем точку К" как точку пересечения M"N" и А"В". Находим точку К' и определяем видимость.

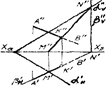
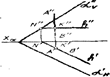
На рис. 3.45 плоскость а задана следами. Прямая, пересекающая плоскость a, является горизонталью, Через прямую АВ проводим горизонтальную плоскость b(b||Н). Плоскость р пересекает плоскость а по горизонтали NK, принадлежащей плоскости a Затем определяем видимость. На рис. 3.46 плоскость а задана следами; прямая АВ, пересекающая плоскость а, горизонтально - проецирующая, на плоскость Н она проецируется в точку и, следовательно, горизонтальная проекция точки пересечения прямой АВ и плоскости a(К¢) находится в этой точке.

A'=B=K', Положение К" определяется при помощи горизонтали.